空间夹角的计算VIP免费

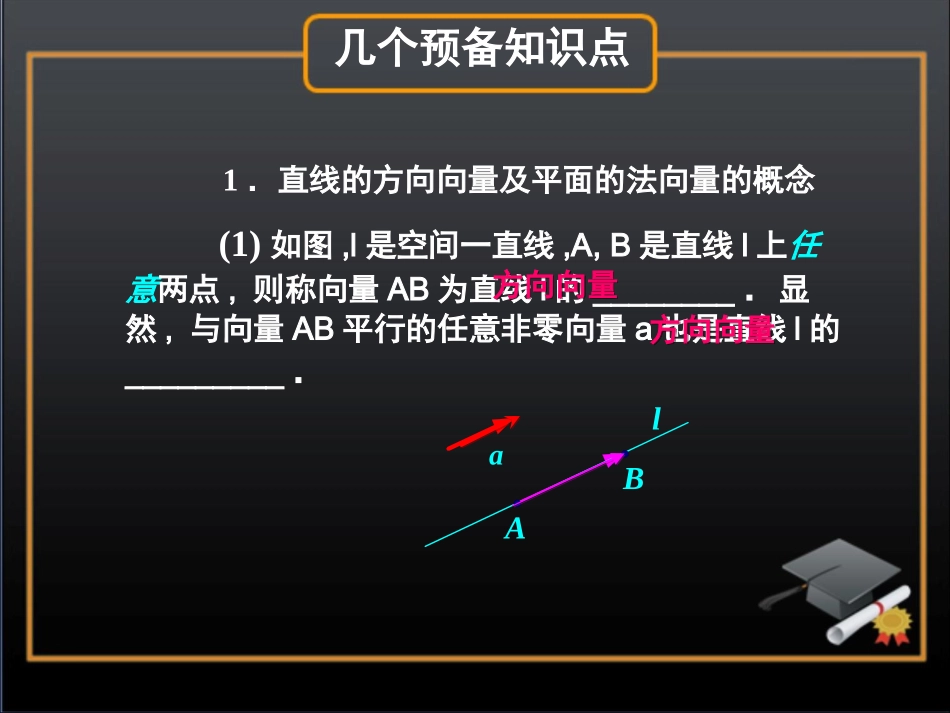
夹角的计算红旗中学----姚辉1．直线的方向向量及平面的法向量的概念几个预备知识点(1)如图,l是空间一直线,A,B是直线l上任意两点,则称向量AB为直线l的________．显然,与向量AB平行的任意非零向量a也是直线l的_________．方向向量方向向量方向向量方向向量laAB(2)如图,如果直线l垂直于平面α,那么把直线l的方向向量n叫作平面α的________．几个预备知识点法向量法向量ααAAlln几个预备知识点2.空间向量的模、夹角的坐标表示设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则（1）|a|＝a·a＝，（2）cos〈a，b〉＝a·b|a||b|＝.（3）a⊥b⇔a·b＝0⇔————————＝0(a，b均为非零向量)．a12＋a22＋a32a1b1＋a2b2＋a3b3a12＋a22＋a32b12＋b22＋b32a1b1＋a2b2＋a3b3几个预备知识点2.若由相交直线a与b确定的平面为α，则如何求平面α的一个法向量n？【提示】向量n满足则n是平面α的法向量0≤〈a，b〉≤π0≤〈a，b〉≤π1.向量a与b的夹角的范围是———————.一、直线的夹角夹角的再认识三、两个平面的夹角二、直线与平面的夹角一、直线的夹角夹角的再认识._______)1(212121的夹角与叫作直线的角在范围交角中与共面时与当直线ll，，ll，ll._______.,A,,)2(212112121的范围是的夹角与异面直线注意的夹角与叫作异面直线的夹角与则平行于作上的任意一点过为异面直线时与当ll：ll，lABlABlll]20,].2(0,二、直线与平面的夹角夹角的再认识找一条直线与平面的夹角，要过直线上一点向平面作垂线，关键是要找到垂足落在何处，才好找出直线与平面的夹角。注意:直线与平面所成角的范围是]20,三、两个平面的夹角夹角的再认识._________：.,,,212121212121范围的夹角与平面的夹角与叫作平面的夹角与则直线与的垂线内作直线与分别在平面上的任意一点过的交线与平面平面如图lllllAll，12l2l1lA]2，[0夹角的计算l1sm2s(1),lm的夹角为，ml设直线l,m的方向向量分别为21,coscosss则21,ss1s2s夹角的计算lm1s2s(1),lm的夹角为，ml设直线l,m的方向向量分别为21,ss1s2s2121cosssss即ulaula夹角的计算1n2n，的夹角为,)2(21,nn平面,的法向量分别为21,nn夹角的计算，的夹角为,)2(21,nn平面,的法向量分别为21,nn1n2n夹角的计算lm1s2s(1),lm的夹角为，ml设直线l,m的方向向量分别为21,ss1s2s2121cosssss即ula，的夹角为,l||||||)2cos(uauaula夹角的计算夹角的计算，的夹角为,)2(21,coscosnn则平面,的法向量分别为21,nn2n1n1n2n夹角的计算夹角的计算，的夹角为,)2(2121cosnnnn即2n1n1n2n平面,的法向量分别为21,nn课堂互动讲练如图,在空间直角坐标系中有长方体ABCD－A'B'C'D',AB＝2,BC＝1,AA'＝3.求对角线AC'和侧面对角线A'D的夹角的余弦值．例例11xyzCC'B'BD'DD'DA'(A)O如图,在空间直角坐标系中有长方体ABCD－A'B'C'D',AB＝2,BC＝1,AA＝3.求对角线AC'和侧面对角线A'D的夹角的余弦值．若改变建系的方式，选择以点B为坐标原点，结论会变吗？课堂互动讲练例例11CC'B'(B)OD'DA'Axyz课堂互动讲练如图,在空间直角坐标系中有单位正方体ABCD－A‘B’C‘D’.求：（1）直线D‘C’与平面D’CBA’的夹角（2)平面BCD'A'与平面ABCD的夹角.例例22D'C'CDB'BA'(A)Oxyz课堂互动讲练如图所示，直三棱柱ABC－A1B1C1，底面△ABC中，CA＝CB＝1，∠BCA＝90°，棱AA1＝2，M，N分别是A1B1，A1A的中点．(1)求异面直线BA1与CB1的夹角的余弦值；(2)求平面NBC1与平面BB1C1的夹角的余弦值.练习练习课堂互动讲练【点评】课堂互动讲练(1)通过求向量BA1→与CB1→的夹角来求异面直线BA1与CB1的夹角；(2)两个平面NBC1与BB1C1的法向量夹角的余弦的绝对值，即为所求.1．求空间两条直线的夹角时可以这样算：规律方法总结.,.cos向量为空间两条直线的方向为空间两条直线的夹角其中ba，baba2．求直线与平面的夹角时可以这样算：规律方法总结，的夹角为...