四直角三角形射影定理VIP免费

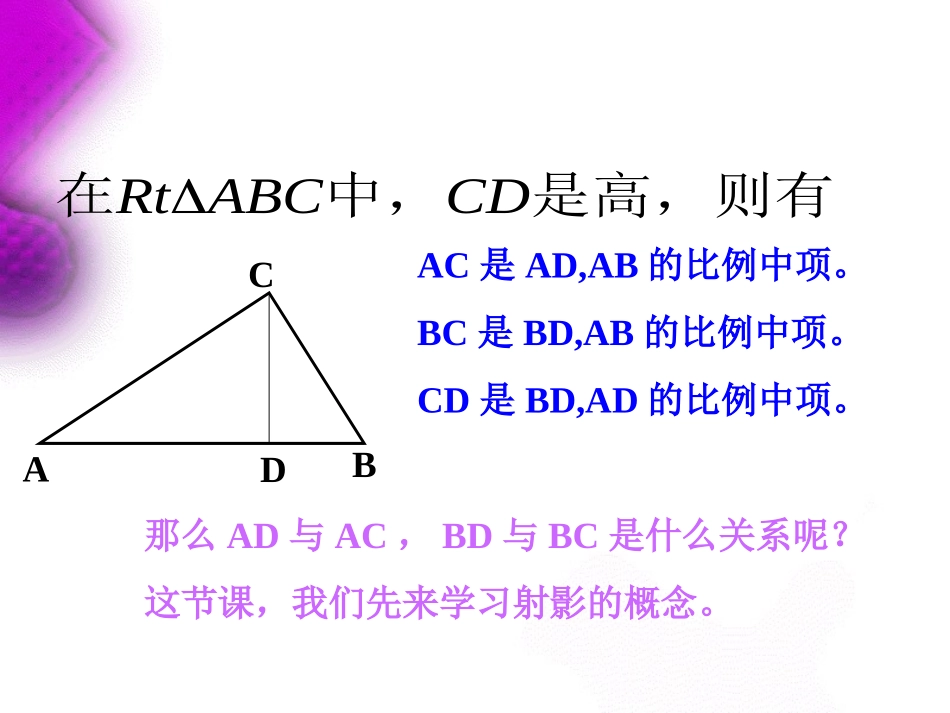
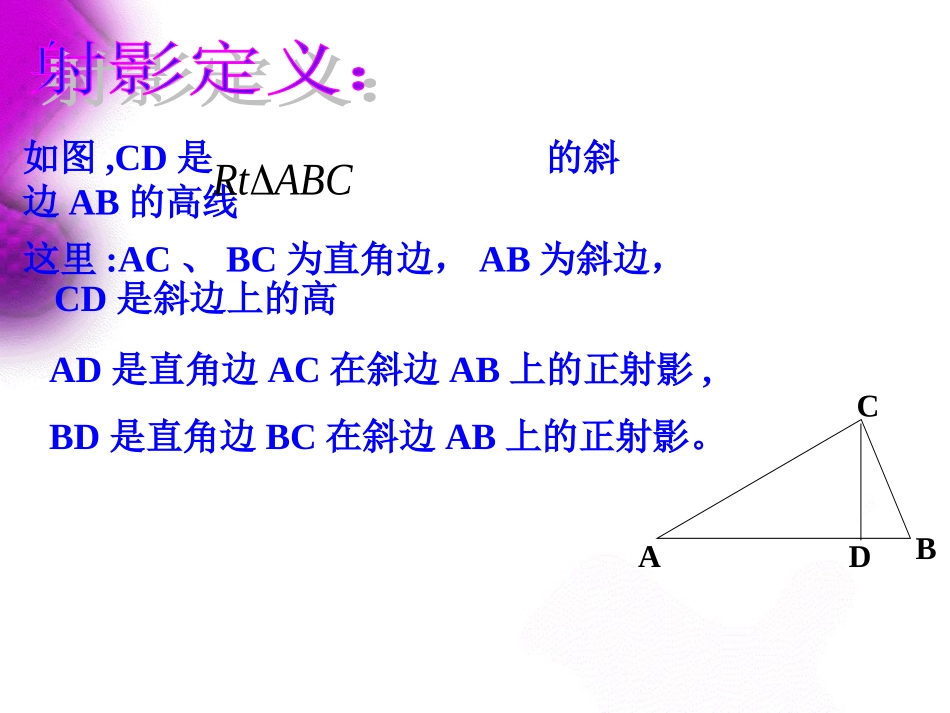
直角三角形的射影定理直角三角形的射影定理CADB是高，则有中，在CDABCRtAC是AD,AB的比例中项。BC是BD,AB的比例中项。CD是BD,AD的比例中项。那么AD与AC，BD与BC是什么关系呢？这节课，我们先来学习射影的概念。如图,CD是的斜边AB的高线ABCRt这里:AC、BC为直角边，AB为斜边，CD是斜边上的高AD是直角边AC在斜边AB上的正射影,BD是直角边BC在斜边AB上的正射影。CADBABADAC2ABBDBC2DBADCD2CADB用文字如何叙述？直角三角形中,斜边上的高线是两条直角边在斜边上的射影的比例中项,每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.这就是射影定理CADB具体题目运用：ACBCCDAB根据应用选取相应的乘积式。ABADAC2ABBDBC2DBADCD2利用射影定理证明勾股定理:222ABABBDABADBCAC射影定理只能用在直角三角形中,且必须有斜边上的高CADB这里犯迷糊，可不行！如图,若AD=2cm,DB=6cm,求CD，AC,BC的长。例1解:答:CD,AC,BC的边长分别为cmcmcm34,4,32CADB分析：利用射影定理和勾股定理;3212,12622cmCDDBADCD;416,166222cmACABADAC.3448,486262cmBCABBDBC(1)在中,CD为斜边AB上的高,图中共有6条线段ABCRtAC,BC,CD,AD,DB,AB已知任意两条,便可求出其余四条.(2)射影定理中每个乘积式中,含三条线段,若已知两条可求第三条.(3)解题过程中,注意和勾股定理联系,选择简便方法.你都弄懂了吗？CEFFBCDF:,求证于∽例2.如图,在中,ABC,,EACDEDABCD于于.CBA分析:欲证CEF∽.CBA公共角ECFACB已具备条件要么找角,要么找边.CACFCBCECEADFBCEFBCFEA或证法一：例2.如图,在中,ABC,,EACDEDABCD于于.CBACEFFBCDF:,求证于∽ACDEABCDCACECD2BCDFABCDCBCFCD2CACFCBCEBCAECF∽.CBACEFCEADFB证法二：四点共圆找角