数列的概念与简单的表示方法VIP免费

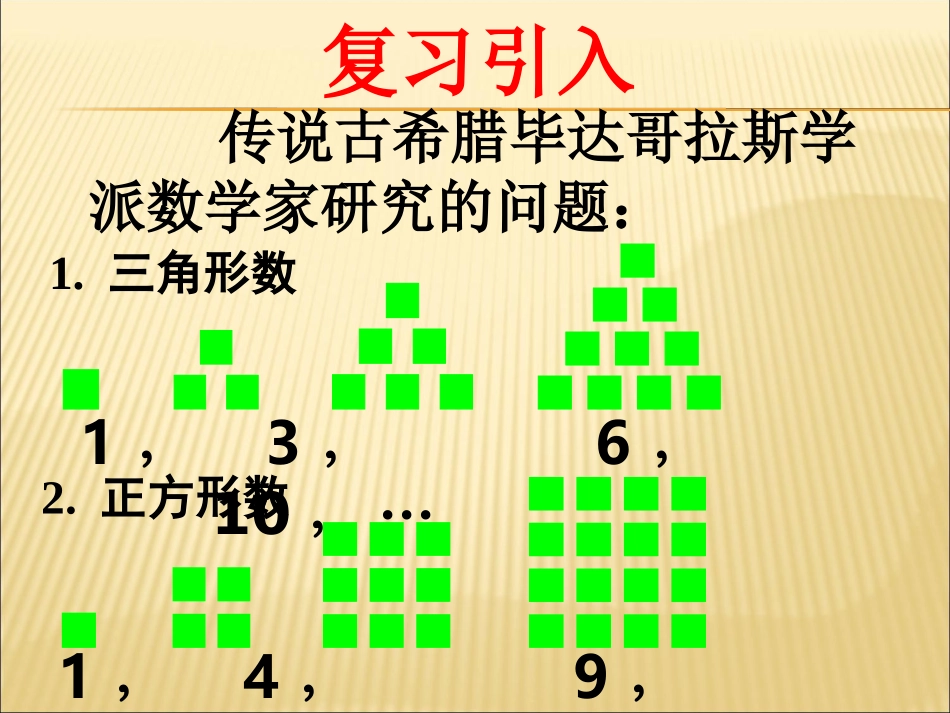
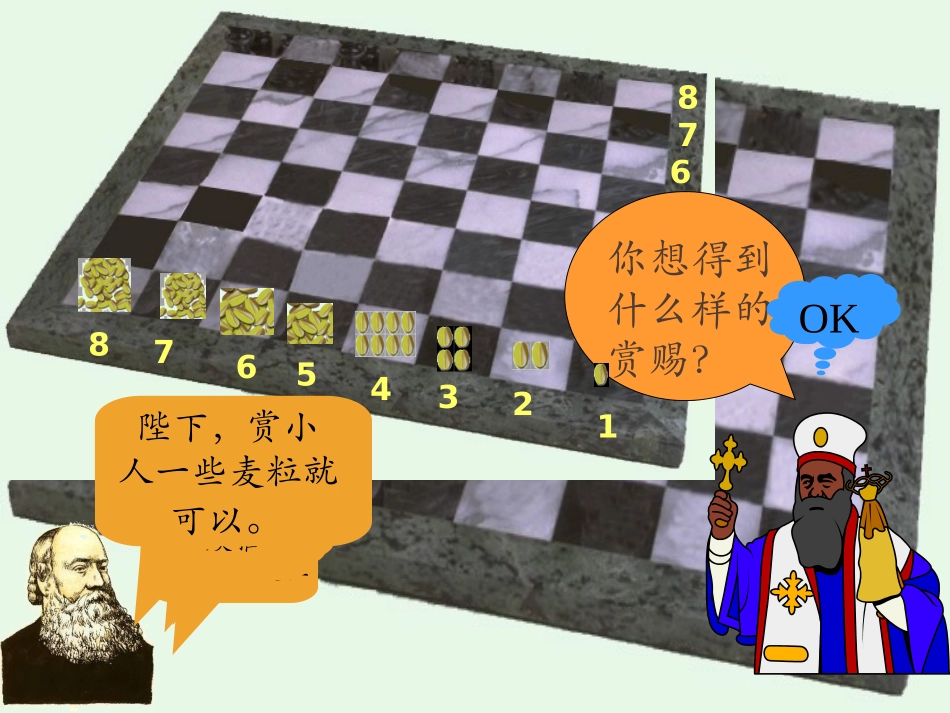
1.三角形数2.正方形数传说古希腊毕达哥拉斯学派数学家研究的问题：复习引入1，3，6，10，···1，4，9，16，···64个格子1223344551667788你想得到什么样的赏赐？OK请在第一个格子放1颗麦粒请在第二个格子放2颗麦粒请在第三个格子放4颗麦粒请在第四个格子放8颗麦粒依次类推……陛下，赏小人一些麦粒就可以。?456781567812334264个格子你认为国王有能力满足上述要求吗每个格子里的麦粒数都是前一个格子里麦粒数的2倍且共有64格子2213263220212?18446744073709551615上述棋盘中各格子里的麦粒数按先后次序排成一列数：633222221，，，，，，，，4131211504321,，，，，1，2，3，4……的倒数排列成的一列数：高一（）班每次考试的名次由小到大排成的一列数：-1的1次幂，2次幂，3次幂，……排列成一列数：1111，，，，，，，1111无穷多个1排列成的一列数：三角形数：1，3，6，10，···正方形数：1，4，9，16，···请观察请观察633222221，，，，354321，，，，1111，，，，，，，1111共同特点共同特点：1.都是一列数；2.都有一定的顺序12345，41，31，211，1，3，6，10，···1，4，9，16，···定义：按一定顺序排列着的一列数称为数列，2，改为13，…，35,2，，…，35331请问：是不是同一数列？数列4改为：-1，1，-1，1……1，-1，1，-1……，请问：是不是同一数列？(数列具有有序性)数列定义定义剖析集合讲究：无序性、互异性、确定性，数列讲究：有序性、可重复性、确定性.12345，，，，1111354321，，，，，，，，4131211633222221，，，，1111，，，数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项(首项)，第2项，······，第n项，······数列的分类(1)按项数分：项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系：递增数列，递减数列，摆动数列，常数列。有穷数列无穷数列有穷数列无穷数列无穷数列递增数列递增数列递减数列摆动数列常数列数列定义数列定义数列的一般形式可以写成：简记为，，，，，naaaa321na项是数列的第nan项是数列的第11a也称为数列的首项项第11a第1项第2项第3项第n项n)1-(1a2a3ana)64,(*nNn}{n1{}n)35,(*nNnna12nnan1nanna123451111-1,,,,,22,12n632,,,,2131n1,,,,23n,,,,3511-,,,,,11,,,1,12n)1(-)(*Nn)(*Nn12n观察这些数列中相遇序号的关系？试一试看你能不能得出它们的通项公式？na或0nnan1)(*Nn每个序号也都对应着一个数（项）例1.写出下面数列的一个通项公式，使它的前4项分别是下列各数：nann1)1(1）（1)1(12nna）（.0,2,0,2)2(;41,31,21,1)1(根据下面数列的前几项的值，写出数列的一个通项公式：练习.521,421,321,221,121)5(;,41,42,21,22,1)4(;,1,0,1,0,1,0)3(;,9910,638,356,154,32)2(;,11,9,7,5,3)1(例2.写出数列的一个通项公式，并判断它的增减性.113）（nnan,135,104,73,42,1例3.根据下面数列{an}的通项公式，写出前五项：.)1()2(;1)1(nannannn练习练习小结1、数列的有关概念2、数列的通项公式；