向量减法运算及其几何意义VIP免费

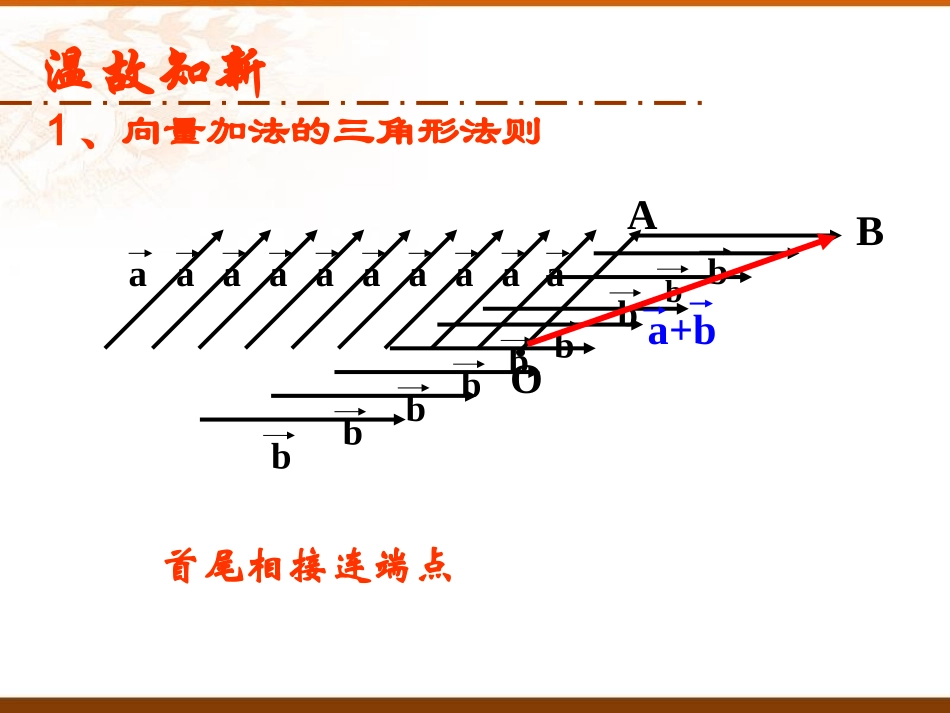
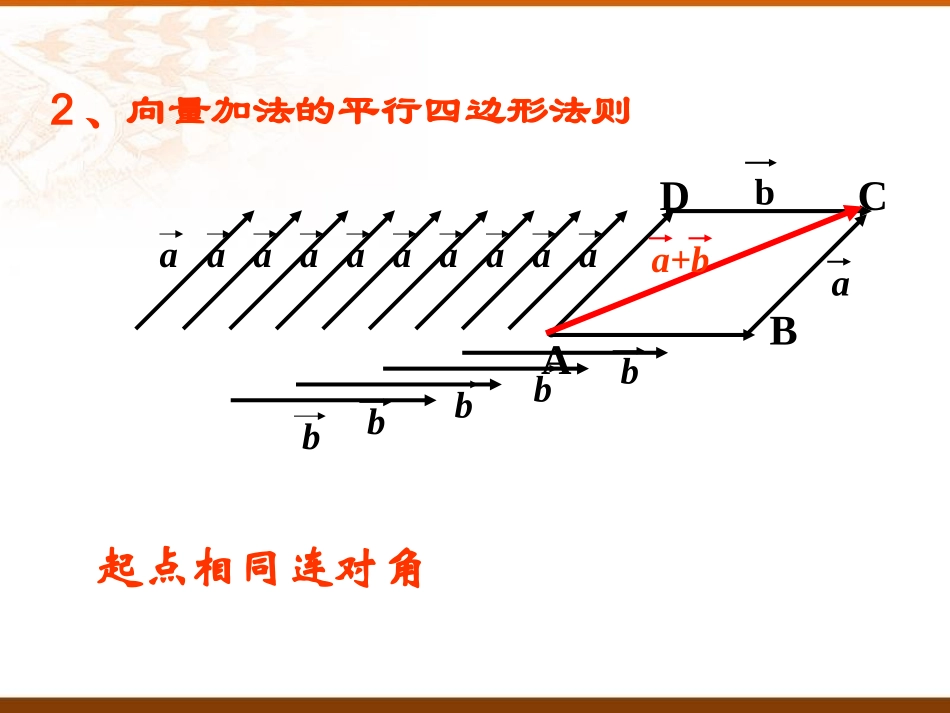
2.2.2向量减法运算及其几何意义1、向量加法的三角形法则baOaaaaaaaabbbbbbbBbaAa+b首尾相接连端点温故知新baAaaaaaaaabbbBbaDaCba+b2、向量加法的平行四边形法则起点相同连对角复习:向量的加法运算及其几何意义.ABCDEFCFBEBCADAB练习1在三角形ABC中，点D，E，F分别为各边的中点，则________.解：CFBEBCADABACADDCADBDADEDBEADBEEDADBEAFADBECFBCAB)()(练习2•已知正方形ABCD的边长为1，cba,,，则bBCcACaABABCD2222cACcba新课F2FF11F�F�已知：两个力的合力为,其中一个力为2F�求：另一个力12FFF�21FFF�21()FFF�(1)向量减法的定义:()abab即减去一个向量相当于加上这个向量的相反向量.(3)向量减法的几何意义:abaOAbBDCb()ab()ab:ab的作图方法(3)向量减法的几何意义:abaOAbBab,.OAOBBA��:表示向量减法的几何意义从向量的终点指向向量的终点的向量abba①将两向量平移,使它们有相同的起点.②连接两向量的终点.③箭头的方向是指向“被减数”的终点.二、向量减法的三角形法则OABabba1O在平面内任取一点2OAa,OBb�作3ab�则向量BA.注意：共起点，连终点，指向前向量的减法•特殊情况1.共线同向2.共线反向abBACababABCab例１：•如图，已知向量a,b,c,d,求作向量a-b,c-d.abcdabcdOABCDabcd��例2：选择题：()()()()ABACDBAADBACCCDDDC��（2）()()()()ABBCADAADBCDCDBDDC��（1）DC,,:,,,,.ABCDABaADbabACDB��如图平行四边形中试用表示向量例3ABCDabbaADABAC解:baADABDB,,,,ABCDABaDAbOCcbcaOA����如图平行四边形例4：证明：ABCDabcOOABAOBABOBacbOBCBOCOCDAcb证明：练习2CDBDACAB化简)1(0:CDCDCDBDCB原式解COBOOCOA化简)2(BAOBOACOOCBOOA0)()()(:原式解,,120||||3||||oABaADbDABababab�如图已知向量练习3:，，且，求和120oabADBCO`|ba||DB||ba||AC|baDBbaAC3|AB||AD|ABCDADAB，故，由向量的加减法知，故此四边形为菱形由于，为邻边作平行四边形、解：以120oabADBCO`333||||sin60322oAODODAD�由于菱形对角线互相垂直平分,所以是直角三角形，33|ba|3|ba|，所以3|AC|ADC60DAC120DABOO是正三角形，则所以，所以因为return练习4：如图,中,你能用表示向量AC和DB吗?ABCD�aAB=,AD=b,,baabABCD解:AC=a+b;DB=a-b.变式训练一：当a,b满足什么条件时，a+b与ab垂直？_____________||||ab变式训练二：当a,b满足什么条件时，|a+b|=|ab|？_____________________ab和互相垂直变式训练三：a+b与ab可能是相等向量吗？___________________________________________abABCD不可能.因为平行四边形的两条对角线方向不同.的夹角？平分向量满足什么条件时，能使当非零向量b,abab,a变式训练四：ba•变式训练五的夹角为多少度？与则若baa,baba30°(一)知识1．理解相反向量的概念2.理解向量减法的定义，3.正确熟练地掌握向量减法的三角形法则小结:(二)重点重点：向量减法的定义、向量减法的三角形法则作业：作业本34-35页1-11