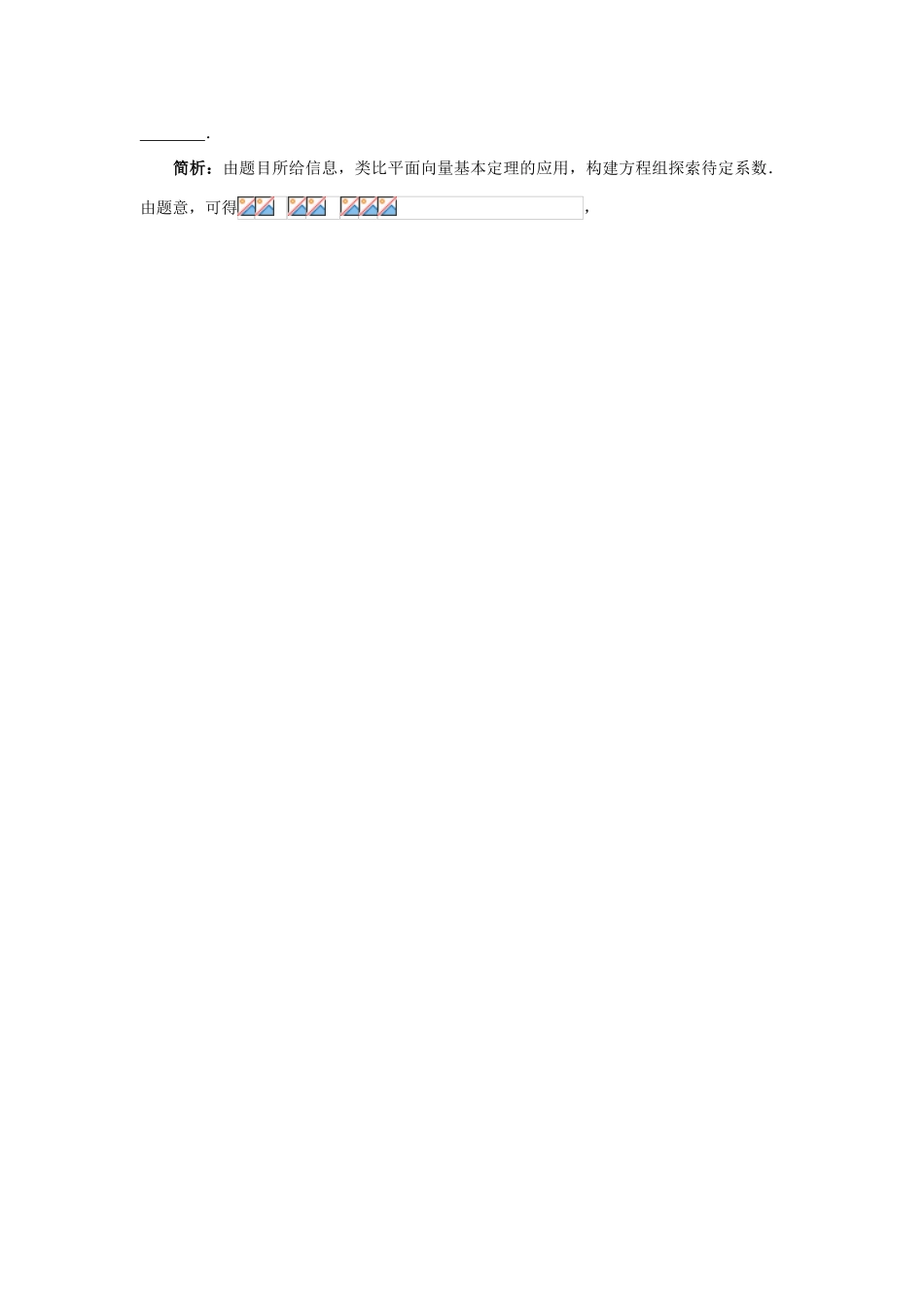
平面向量综合问题求解策略1.利用向量的概念和加、减法法则及意义转化例1已知向量,,则的最大值为.简析:利用平面向量的概念和坐标运算,将向量模的最值转化为三角函数的最值,体现了等价转化,即把“向量问题函数化”.,,当时,.2.利用向量垂直转化例2三角形满足,试判断三角形的形状.简析:从平面向量的运算和数量积的意义切入,利用向量垂直的条件使问题简单化.把代入已知得,,而均不是零向量,则,,即为直角三角形.3.利用实数与向量的积和两个向量共线的条件转化例3已知为坐标原点,点,点的坐标分别为,其中常数,点在线段上,且,求的最大值.简析:利用共线和数量积的坐标表示,可以转化为求函数的最值问题,,,即为所求最大值.4.类比平面向量的基本定理的应用进行转化例4若对个向量存在个不全为0的实数,使得成立,则称为线性相关,依此规定线性相关的实数可取出的一组数据为.简析:由题目所给信息,类比平面向量基本定理的应用,构建方程组探索待定系数.由题意,可得,故实数可取出的一组数据为.5.活用向量的数量积的几种不同的运算转化例5平面内有向量,点为直线上的一个动点.(1)当取最小值时,求的坐标;(2)当点满足(1)的条件和结论时,求的值.简析:用向量的运算将数量积的坐标表示化为函数问题.(1)设,在直线上,向量共线.又,..时,有最小值时,此时.(2)当时,,,,.