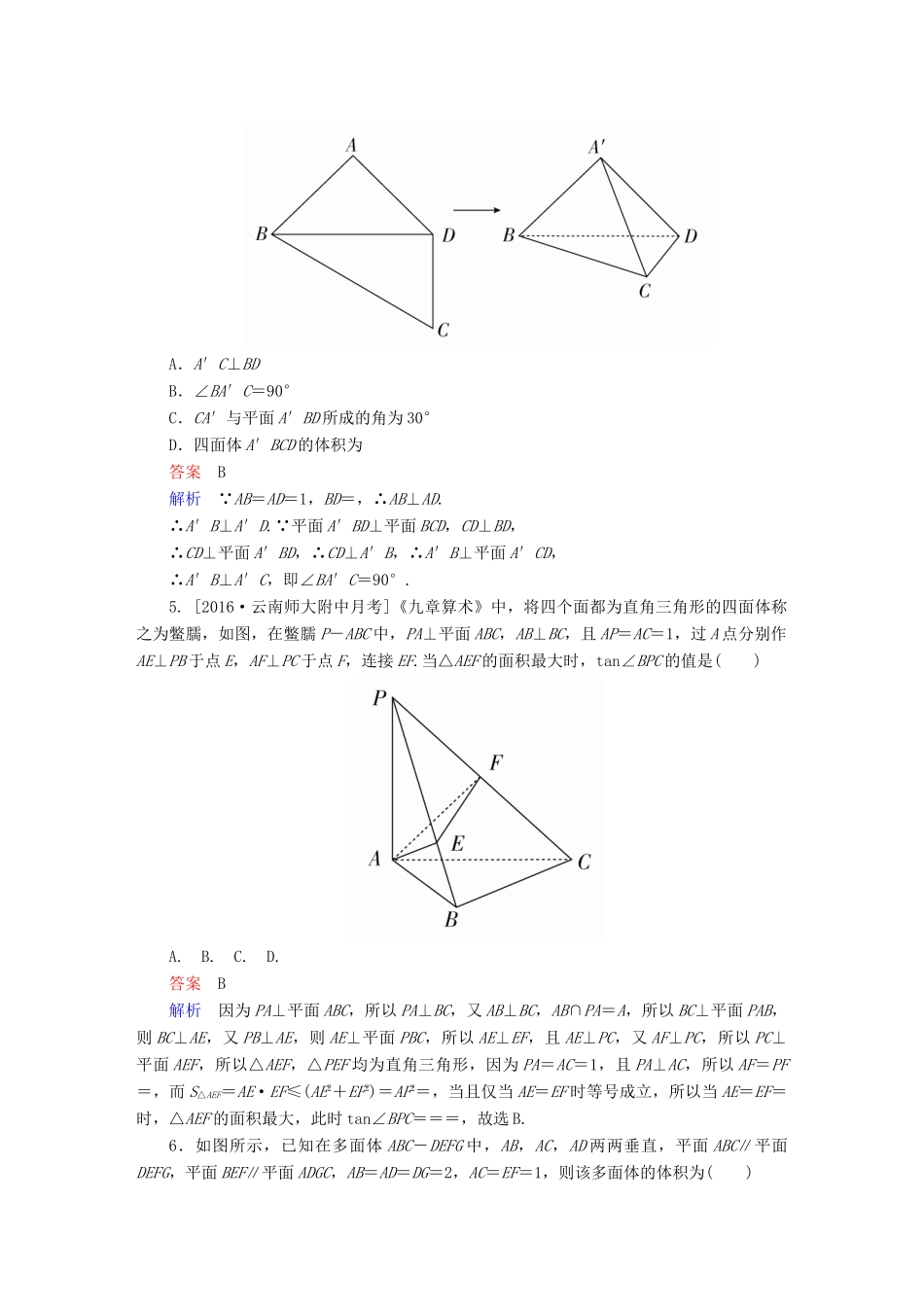
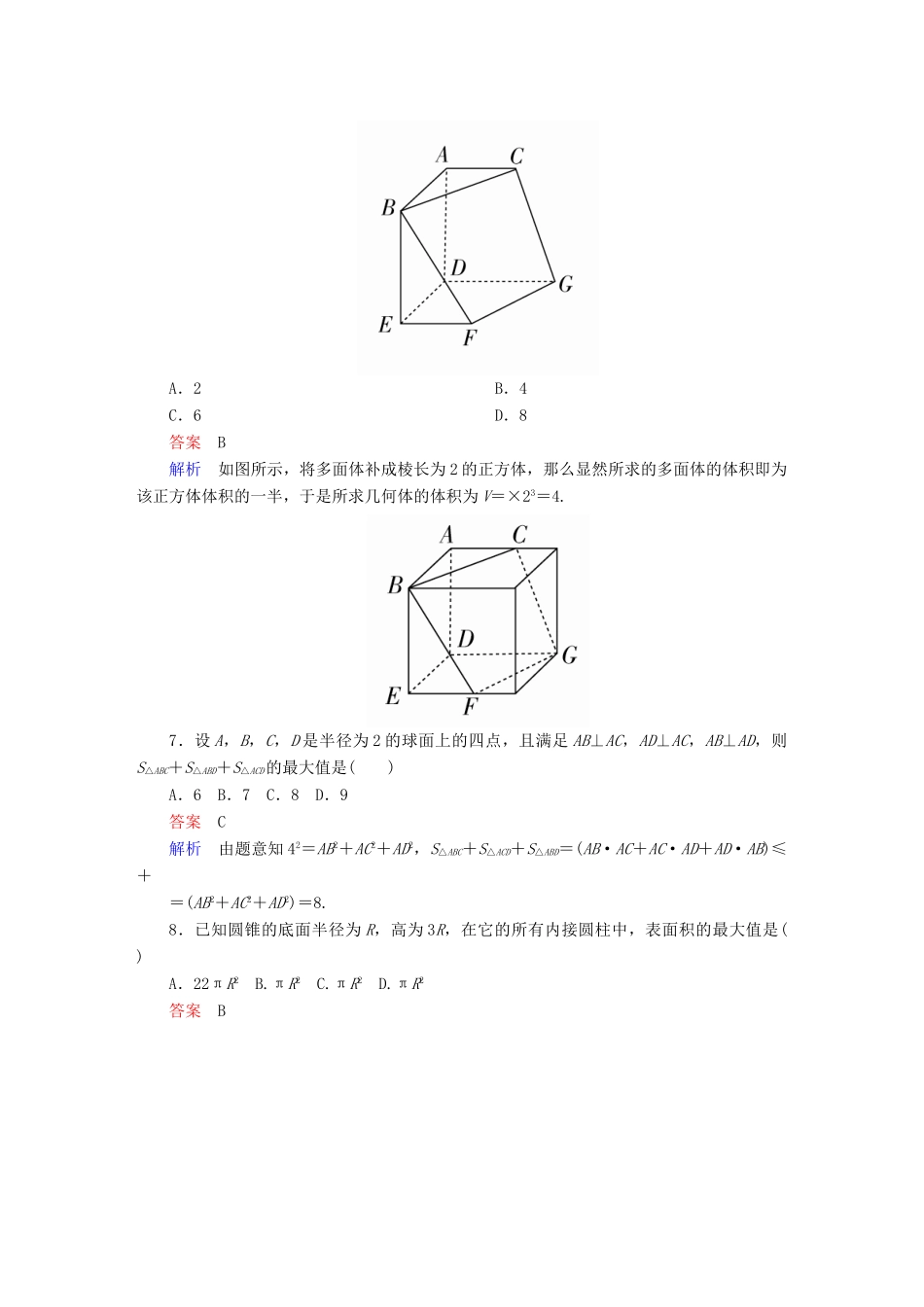
专题突破练(5)立体几何的综合问题一、选择题1.已知直线a⊂平面α,直线b⊂平面β,则“a∥b”是“α∥β”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件答案D解析“a∥b”不能得出“α∥β”,反之由“α∥β”也得不出“a∥b”.故选D.2.如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,A1A=AB=2,BC=1,AC=,若规定正视方向垂直平面ACC1A1,则此三棱柱的侧视图的面积为()A.B.2C.4D.2答案A解析在△ABC中,AC2=AB2+BC2=5,∴AB⊥BC.作BD⊥AC于D,则BD为侧视图的宽,且BD==,∴侧视图的面积为S=2×=.3.平行六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为()A.3B.4C.5D.6答案C解析如图,既与AB共面也与CC1共面的棱有CD、BC、BB1、AA1、C1D1,共5条.4.在四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是()A.A′C⊥BDB.∠BA′C=90°C.CA′与平面A′BD所成的角为30°D.四面体A′BCD的体积为答案B解析 AB=AD=1,BD=,∴AB⊥AD.∴A′B⊥A′D. 平面A′BD⊥平面BCD,CD⊥BD,∴CD⊥平面A′BD,∴CD⊥A′B,∴A′B⊥平面A′CD,∴A′B⊥A′C,即∠BA′C=90°.5.[2016·云南师大附中月考]《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑P-ABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于点E,AF⊥PC于点F,连接EF.当△AEF的面积最大时,tan∠BPC的值是()A.B.C.D.答案B解析因为PA⊥平面ABC,所以PA⊥BC,又AB⊥BC,AB∩PA=A,所以BC⊥平面PAB,则BC⊥AE,又PB⊥AE,则AE⊥平面PBC,所以AE⊥EF,且AE⊥PC,又AF⊥PC,所以PC⊥平面AEF,所以△AEF,△PEF均为直角三角形,因为PA=AC=1,且PA⊥AC,所以AF=PF=,而S△AEF=AE·EF≤(AE2+EF2)=AF2=,当且仅当AE=EF时等号成立,所以当AE=EF=时,△AEF的面积最大,此时tan∠BPC===,故选B.6.如图所示,已知在多面体ABC-DEFG中,AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为()A.2B.4C.6D.8答案B解析如图所示,将多面体补成棱长为2的正方体,那么显然所求的多面体的体积即为该正方体体积的一半,于是所求几何体的体积为V=×23=4.7.设A,B,C,D是半径为2的球面上的四点,且满足AB⊥AC,AD⊥AC,AB⊥AD,则S△ABC+S△ABD+S△ACD的最大值是()A.6B.7C.8D.9答案C解析由题意知42=AB2+AC2+AD2,S△ABC+S△ACD+S△ABD=(AB·AC+AC·AD+AD·AB)≤+=(AB2+AC2+AD2)=8.8.已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,表面积的最大值是()A.22πR2B.πR2C.πR2D.πR2答案B解析如图所示,为组合体的轴截面,记BO1的长度为x,由相似三角形的比例关系,得=,则PO1=3x,圆柱的高为3R-3x,所以圆柱的表面积为S=2πx2+2πx·(3R-3x)=-4πx2+6πRx,则当x=R时,S取最大值,Smax=πR2.9.在正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,M,N分别为AB,BC边的中点,点Q为平面ABCD内一点,线段D1Q与OP互相平分,则满足MQ=λMN的实数λ的值有()A.0个B.1个C.2个D.3个答案C解析本题可以转化为在MN上找点Q使OQ綊PD1,可知只有Q点与M,N重合时满足条件,所以选C.10.[2016·河北唐山模拟]四棱锥M-ABCD的底面ABCD是边长为6的正方形,若|MA|+|MB|=10,则三棱锥A-BCM的体积的最大值是()A.16B.20C.24D.28答案C解析 三棱锥A-BCM体积=三棱锥M-ABC的体积,又正方形ABCD的边长为6,S△ABC=×6×6=18,又空间一动点M满足|MA|+|MB|=10,M点的轨迹是椭球,当|MA|=|MB|时,M点到AB距离最大,h==4,∴三棱锥M-ABC的体积的最大值为V=S△ABCh=×18×4=24,∴三棱锥A-BCM体积的最大值为24,故答案为C.11.[2016·河北衡水模拟]在一个棱长为4的正方体内,最多能放入的直径为1的球的个数()A.64B.66C.68D.70答案B解析根据球体的特点,最多应该是放5层,第一层能放16个;第2层放在每4个小球中间的...