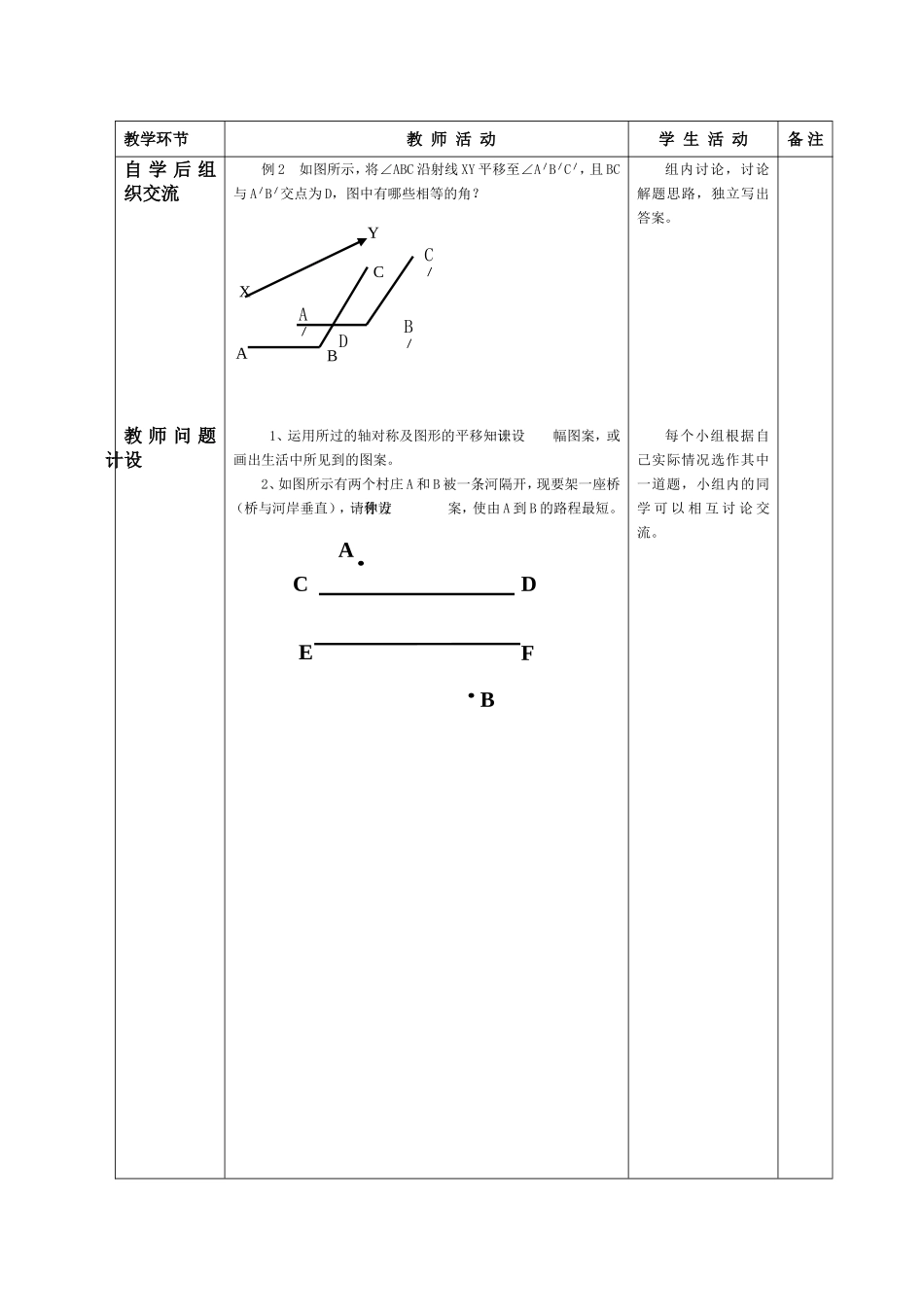
授课时间2010年9月19日授课教师邝朝勇周课时序数5-1课题3.1生活中的平移课型新教学目标知识能力认识平移、理解平移的基本内涵;理解平移前后两个图形对应点连线平行且相等,对应线段平行且相等,对应角相等的性质。过程方法让学生经历观察、分析、操作、欣赏以及抽象概括等过程;经历探索图形平移性质的过程,以及与他人合作交流的过程,进一步发展空间观念,增强审美意识。情感态度价值观通过探究式的学习,培养学生的归纳总结与猜想的数学能力,培养学生的逆向思维能力。通过知识的拓展,培养学生的分析问题与解决问题的能力。教学重点及方法教学重点方法探究平移变换的基本要素,画简单图形的平移图;自学引导教学难点及方法教学难点方法决定平移的两个主要因素。自学引导教学用具教师三角板学生作图工具教学流程设计教师指导学生活动一、教师引导激发学生的学习热情二、引导学生自学教材三、自学后组织交流四、教师问题设计(自学效果检查)五、精选练习,掌握应用:一、课前回顾二、学生自学教材三、自学后交流四、思维训练(试一试)五、掌握应用教学环节教师活动学生活动备注一、教师引导激发学生的学习热情:二、组织学生自学教材引入确定目标展示与平移有关的图片,借助实物演示平移。分析平移定义,探讨“沿某一方向”的意义,其实质是沿直线运动。让学生讨论图中的运动各在那种情况下是平移,图中还有哪些图形可以通过平移得到让学生列举生活中的平移实例,对理解有偏差的加以纠正学生观察静态图片,让学生观察图中具有特殊位置关系的线段,归纳猜想所能得到的结论;利用几何画板实验验证猜想。例1如图所示,△ABE沿射线XY方向平移一定距离后成为△CDF。找出图中平行且相等的线段和全等的三角形。变式练习:如图所示,∠DEF是∠ABC经过平移得到的,∠ABC=33O,求∠DEF的度数。学生分组讨论,如何将所看到的现象用简洁的语言叙述。讨论“沿某一方向”的意义。分组讨论:(1)能否通过平移得到。(2)能平移得到的其基本图形是什么?有哪些方法?列举事例观察猜想,小组同学讨论自己所能得到的结论。分组讨论,找一位同学板书。独立思考解答,组内相互交流。XY教学环节教师活动学生活动备注自学后组织交流教师问题设计例2如图所示,将∠ABC沿射线XY平移至∠A/B/C/,且BC与A/B/交点为D,图中有哪些相等的角?1、运用所过的轴对称及图形的平移知识设计一幅图案,或画出生活中所见到的图案。2、如图所示有两个村庄A和B被一条河隔开,现要架一座桥(桥与河岸垂直),请你设计一种方案,使由A到B的路程最短。组内讨论,讨论解题思路,独立写出答案。每个小组根据自己实际情况选作其中一道题,小组内的同学可以相互讨论交流。XYABCA/B/C/DABCDEF课堂小结1.认识平移、理解平移的基本内涵;2.理解平移前后两个图形对应点连线平行且相等,3.对应线段平行且相等,对应角相等的性质。作业习题3.1及课时达标板书设计图形、定义及基本性质。例题1例题2例题3课后反思本节内容比较简单,学生整体掌握较好。内容贴近生活,学生兴致较高,课堂气氛活跃,参与意识较强。借助多媒体进行实验验证,直观、形象。但对性质的应用欠佳。点评:本节课目标制定恰当,在教学过程中着力于学生能力的培养。充分体现了学生为主体,老师为主导的教学思想;培养学生的思维能力与创新能力。在教学过程中渗透数学美学思想,促进学生综合素质的提高。