43--解直角三角形VIP免费

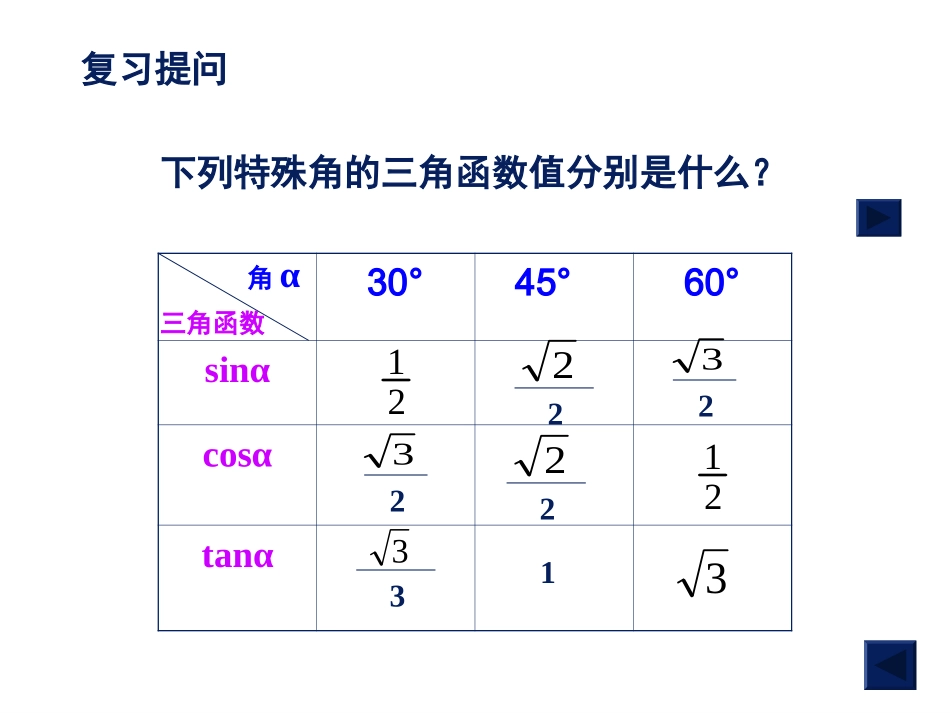
解直角三角形本节内容4.3在图形的研究中，直角三角形是常见的三角形之一，因而人们经常会遇到求直角三角形的边长或角度等问题.对于这类问题，我们一般利用前面已学的锐角三角函数的有关知识来解决.新课导入30°45°60°sinαcosαtanα角α三角函数2122222132323133复习提问下列特殊角的三角函数值分别是什么？如图4-23，在直角三角形ABC中，∠C=90°，∠A，∠B，∠C的对边分别记作a，b，c.图4-23引入新课问题1直角三角形的三边之间有什么关系？a2+b2=c2(勾股定理)a2+b2=c2(勾股定理)图4-23问题2直角三角形的锐角之间有什么关系？∠A+∠B=90°.∠A+∠B=90°.图4-23问题3直角三角形的边和锐角之间有什么关系？图4-23sinAaA==c.∠的对边斜边cosAbcA==.∠的邻边斜边tanAaA==b.∠的对边邻边如果知道的2个元素都是角，不能求解.因为此时的直角三角形有无数多个.如果知道的2个元素都是角，不能求解.因为此时的直角三角形有无数多个.问题4在一个直角三角形中，除直角外有5个元素（3条边、2个锐角），要知道其中的几个元素就可以求出其余的元素？结论在直角三角形中，除直角外的5个元素(3条边和2个锐角)，只要知道其中的2个元素(至少有一个是边)，利用上述关系式，就可以求出其余的3个未知元素，把在直角三角形中利用已知元素求其余未知元素的过程叫作解直角三角形.结论解直角三角形的依据(1)三边之间的关系:a2＋b2＝c2（勾股定理）；(2)锐角之间的关系:∠A＋∠B＝90º；(3)边角之间的关系:tanA＝absinA＝accosA＝bc★面积公式：1122ABCSabch举例例1如图4-24，在Rt△ABC中，a=5，求∠B，b，c.9030,,CA图4-24解:90903060.BA又∵tan=bBa,∴3=tan=5tan60=5baB.∵sin=aAc,∴10sinsin55====1302Aac.举例例2如图，在Rt△ABC中，∠C=90°，cosA=，BC=5，试求AB的长..13cos01c=90,A=,3解∵：∠分析：在直角三角形中，已知一边和另两边的关系，常用勾股定理方程思想解决.AC1=AB3∴1AB=x,AC=x.3设则2222221AB=AC+BC,x=x+53又即12152152x=,x=-44∴（舍去）152AB.4∴的长为分析：已知角和线段都不在直角三角形中，所以需分别延AD、BC,交于点E，从而解的直角三角形ABE即可.例4在四边形ABCD中，∠A=，AB⊥BC，AD⊥DC，AB=20，CD=10，求AD，BC的长.（保留根号）60°EBACD201060°30°举例ADBC解：40-103,203-2030°14解直角三角形的情况ACBcba归纳1.已知一条边和一个锐角：(1)斜边c和锐角A:(2)直角边a锐角A:AB90AcasinAcbcos22bacAB90Aabtan15ACBcba小结：解直角三角形，只有上面两种情况：一共有四种小的情况。2:已知两条边:(1)斜边c和直角边a：(2)直角边a;bAB9022acbAcaA求;sinAcaA求;sinAB9022bac练习答：cmcm4534.24A=a=c=,,.1.在Rt△ABC中，b=3cm，求∠A，a，c(精确到0.01cm).9045,,CB答：cm83753b=A=B=,,.2.在Rt△ABC中，a=6cm，c=10cm，求b，∠A，∠B(角度精确到1°).90C,答：3cmcm6088B=a=b=,,.3.在Rt△ABC中，c=16cm，求∠B，a，b.9030,,CA4.如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.ABC45030040ΔABCACBCBACS解：42,2(26),105443在遇到解直角三形的问题时，最好先画一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，以得于分析解决问题.选取关系式时要尽量利用原始数据，以防止“累积错误”.解直角三角形的方法遵循“有斜用弦，无斜用切；宁乘勿除，化斜为直”.课堂小结说说解直角三角形时，有哪些注意点？