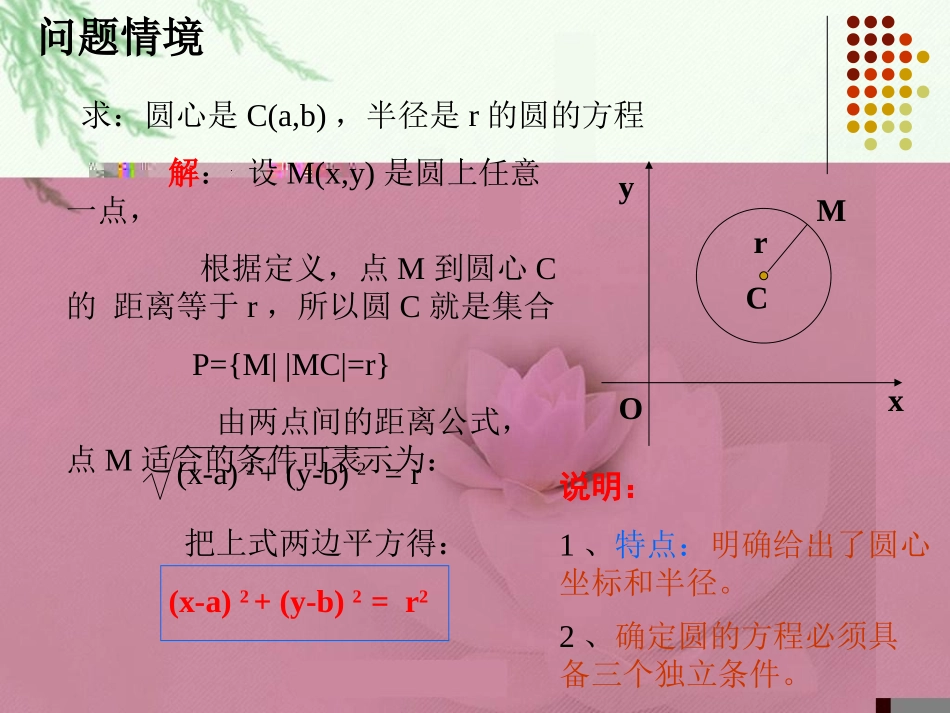
4.1.1圆的标准方程1、掌握圆的标准方程及其推到过程。2、能根据圆心、半径写出圆的标准方程,也能由标准方程写出圆的圆心、半径。本节学习后的目标:求:圆心是C(a,b),半径是r的圆的方程xCMrOy说明:1、特点:明确给出了圆心坐标和半径。2、确定圆的方程必须具备三个独立条件。解:设M(x,y)是圆上任意一点,根据定义,点M到圆心C的距离等于r,所以圆C就是集合P={M||MC|=r}由两点间的距离公式,点M适合的条件可表示为:(x-a)2+(y-b)2=r把上式两边平方得:(x-a)2+(y-b)2=r2问题情境(x-2)2+(y+3)2=5例1、写出圆心为A(2,-3),半径长等于5的圆的方程,并判断点M1(5,-7),M2(-,-1)是否在这个圆上。5补充练习:写出下列各圆的圆心坐标和半径:(1)(x-1)2+y2=6(2)(x+1)2+(y-2)2=9(1,0)6(-1,2)3解:圆心是A(2,3),半径长等于5的圆的标准方程是例题分析求圆心C在直线x+2y+4=0上,且过两定点A(-1,1)、B(1,-1)的圆的方程。(x+)2+(y+)2=3434950例2:求以C(1,3)为圆心,并且和直线3x-4y-7=0相切的圆的方程。CyxOM解:设所求圆的方程为:(x-1)2+(y-3)2=r2因为圆C和直线3x-4y-7=0相切所以圆心C到这条直线的距离等于半径r根据点到直线的距离公式,得|3×1—4×3—7|32+(-4)2=516r=因此,所求圆的方程是(x-1)2+(y-3)2=25256练习2:已知一个圆的圆心在原点,并与直线4x+3y-70=0相切,求圆的方程。x2+y2=196例3已知圆的方程是,求经过圆上一点的切线的方程。222ryx),(00yxM),(00yxMyxO.,),(.,.12002202000000000ryyxxryxMxxyxyyMyxkxykkkkOMOM所求的切线方程是在圆上,所以因为点的切线方程是经过点,解:设切线的斜率为则当点M在坐标轴上时,可以验证,上面方程同样适用.圆的方程是,经过圆上一点的切线的方程222ryx),(00yxMx0x+y0y=r2过圆(x-a)2+(y-b)2=r2上一点M(x0,y0)的切线方程为:(x0-a)(x-a)+(y0-b)(y-b)=r2数学结论练习3:写出过圆x2+y2=10上一点M(2,)的切线方程。6练习4:已知圆的方程是x2+y2=1,求:(1)斜率等于1的切线的方程;2x+y=1062(2)在y轴上截距是的切线方程。y=±x+2所以切线方程为:y=x±2提示:设切线方程为y=x+b,由圆心到切线的距离等于半径1,得:|b|12+(-1)2=1解得b=±2从圆x2+y2=10外一点P(4,2)向该圆引切线,求切线方程。思考题:x+3y=10或3x-y=10课堂小结(1)圆心为C(a,b),半径为r的圆的标准方程为(x-a)2+(y-b)2=r2当圆心在原点时a=b=0,圆的标准方程为:x2+y2=r2(2)由于圆的标准方程中含有a,b,r三个参数,因此必须具备三个独立的条件才能确定圆;(3)注意圆的平面几何知识的运用以及应用圆的方程解决实际问题。