等腰三角形性质及证明VIP免费

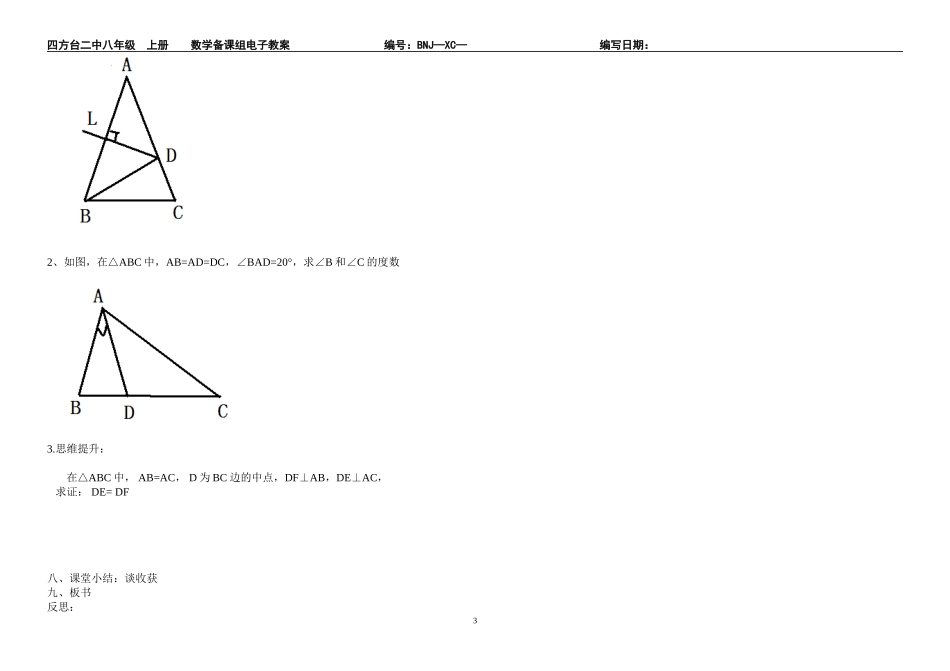
四方台二中八年级上册数学备课组电子教案编号：BNJ—XC—编写日期：13.3.1等腰三角形教学目标：知识与技能：掌握等腰三角形的性质，并能灵活应用等腰三角形的性质解决一些实际问题。过程与方法：通过学生的操作和思考，培养动手操作能力、观察能力、抽象归纳能力。情感态度与价值观：经历应用等腰三角形的相关性质解决实际问题的过程，体会数学与现实的密切联系，感受数学的应用价值，培养应用意识教学重点：等腰三角形的性质及应用．教学难点：等腰三角形三线合一的性质的理解及其应用．教学方法：自主合作探究法．教具准备：多媒体课件、硬纸、剪刀．教学过程：一、复习提问，图片欣赏，导入新课。二、明确学习目标。三、自学课本，理解等腰三角形的性质及证明（或交流补全导学案）。四、回顾等腰三角形的构成要素。．五、自主学习，合作探究（动手操作：同学们拿出自己准备的硬纸和剪刀，根据自学把一张长方形纸片对折，并剪下阴影部分，再把它展开得到一个等腰三角形.）1、把剪出的等腰三角形ABC沿折痕（AD所在的直线）对折后，你发现了什么？找出其中重合的线段和角，填入下表：重合的角重合的线段2、想猜发现等腰三角形有什么性质。性质1：.性质2：.3、讨论研究，验证猜想证明性质1：等腰三角形的两个底角相等.（等边对等角）。这一性质的已知和求证分别是什么？已知：求证：证明：这一性质的几何语言如下：∵∴证明性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（等腰三角形三线合一）这个猜想可以分解成下面三个方面来理解：（1）等腰三角形的顶角的平分线，既是又是。（2）等腰三角形的底边上中线，既是又是。（3）等腰三角形的底边上的高，既是又是。1四方台二中八年级上册数学备课组电子教案编号：BNJ—XC—编写日期：如何证明？（提示：由上面折叠的过程获得启发，我们可以构建两个三角形，从而利用三角形的全等来证明）证明：几何语言：∵∴归纳性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（等腰三角形三线合一）几何语言归纳;(如图)1.∵AB=AC∠1=∠2∴2.∵AB=ACBD=CD∴3.∵AB=ACAD⊥BC∴六、精讲点拔，释疑解难[例1]如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求：△ABC各角的度数．你的方法发现：七、课堂小练（一）做一做：1、等腰三角形一个底角为75°,它的另外两个角为.2、.等腰三角形一个角为110°,它的另外两个角为3、等腰三角形一个角为70°,它的另外两个角为.（二）学以致用：1、如图，在△ABC中，∠A=40°，AB的垂直平分线DE交AB、AC于E、D，则∠DBC的度数为2四方台二中八年级上册数学备课组电子教案编号：BNJ—XC—编写日期：2、如图，在△ABC中，AB=AD=DC，∠BAD=20°，求∠B和∠C的度数3.思维提升：在△ABC中，AB=AC，D为BC边的中点，DF⊥AB，DE⊥AC，求证：DE=DF八、课堂小结：谈收获九、板书反思：3