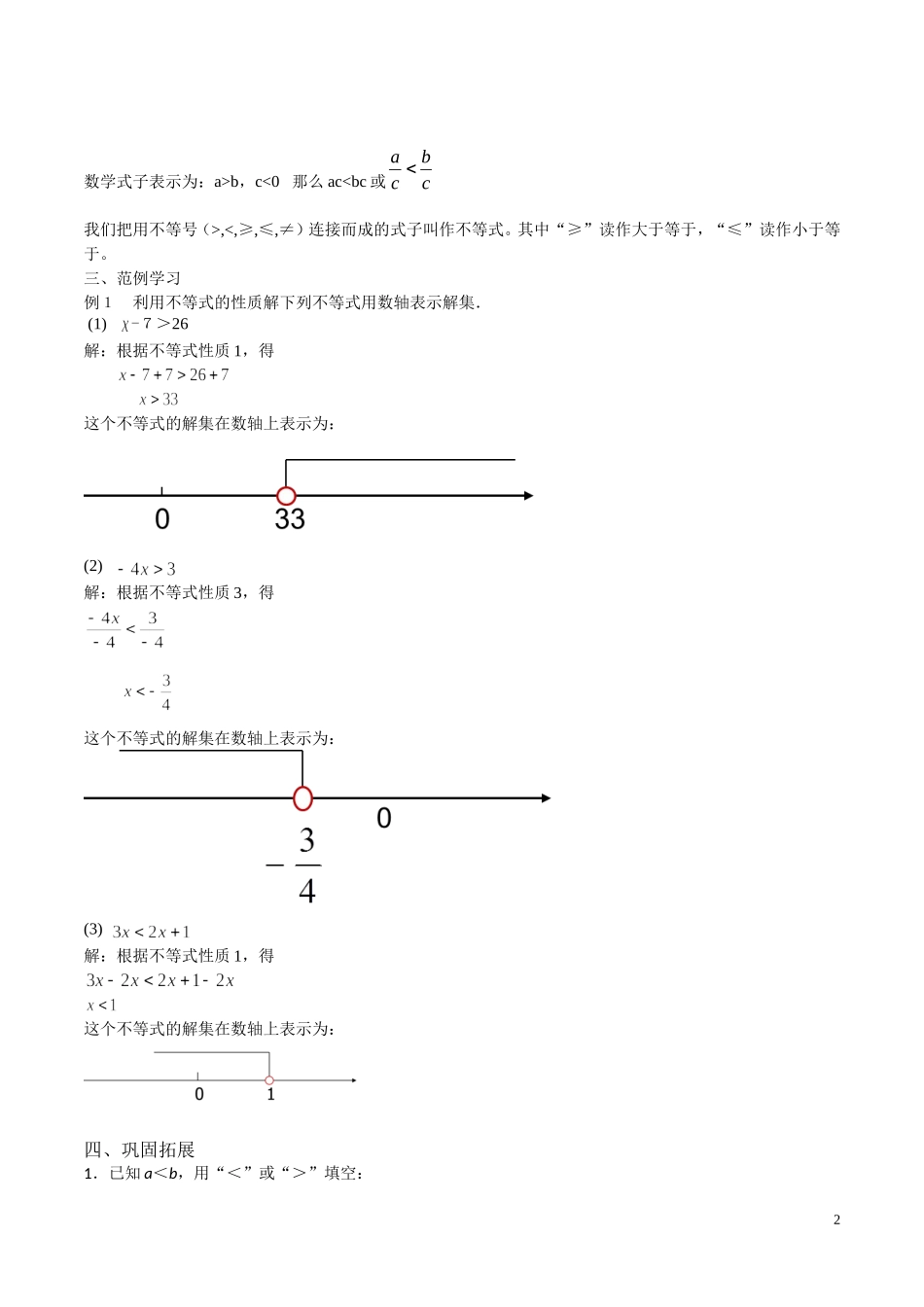
19.1.2不等式的性质教案大理洱源邓川初级中学舒波教学目标:1.理解不等式的性质,掌握不等式的解法.2能熟练的应用不等式的基本性质进行不等式的变形.教学重点:不等式的性质和解法.教学难点:不等号方向的确定.教法:演示法、学法:类比法复习:1.什么是不等式?不等式的解?用“>”或“<”表示大小关系的式子叫做不等式.使不等式成立的未知数的值叫做不等式的解2.什么是不等式解集?能使不等式成立的未知数的取值范围,叫做不等式的解的集合,简称解集.一、情境引入(1)观察:用“<”或“>”填空,并找一找其中的规律.5>35+2>3+25-2>3-2–1<3-1+2<3+2-1-3<3-3不等式两边加(或减)同一个数,不等号的方向不变。6>26×3>2×36÷2>2÷2–2<3(-2)×6<3×6(-2)÷2<3÷2不等式的两边乘以(或除以)同一个正数,不等号的方向不变。6>26×(-2)<2×(-2)6÷(-2)<2÷(-2)–2<4(-2)×(-2)>4×(-2)(-2)÷(-2)>4÷(-2)不等式的两边乘以(或除以)同一个负数,不等号的方向改变。二、互动新授不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变。数学式子表示为:a>b,那么a±c>b±c不等式性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变。数学式子表示为:a>b,c>0;ac>bc或cbca不等式性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变。2数学式子表示为:a>b,c<0那么ac,<,≥,≤,≠)连接而成的式子叫作不等式。其中“≥”读作大于等于,“≤”读作小于等于。三、范例学习例1利用不等式的性质解下列不等式用数轴表示解集.(1)-7>26解:根据不等式性质1,得这个不等式的解集在数轴上表示为:(2)解:根据不等式性质3,得这个不等式的解集在数轴上表示为:(3)解:根据不等式性质1,得这个不等式的解集在数轴上表示为:四、巩固拓展1.已知a<b,用“<”或“>”填空:3(1)a+3b,那么a±c>b±c不等式性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变。4数学式子表示为:a>b,c>0;ac>bc或cbca不等式性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变。数学式子表示为:a>b,c<0那么ac