立体几何中的最值问题VIP免费

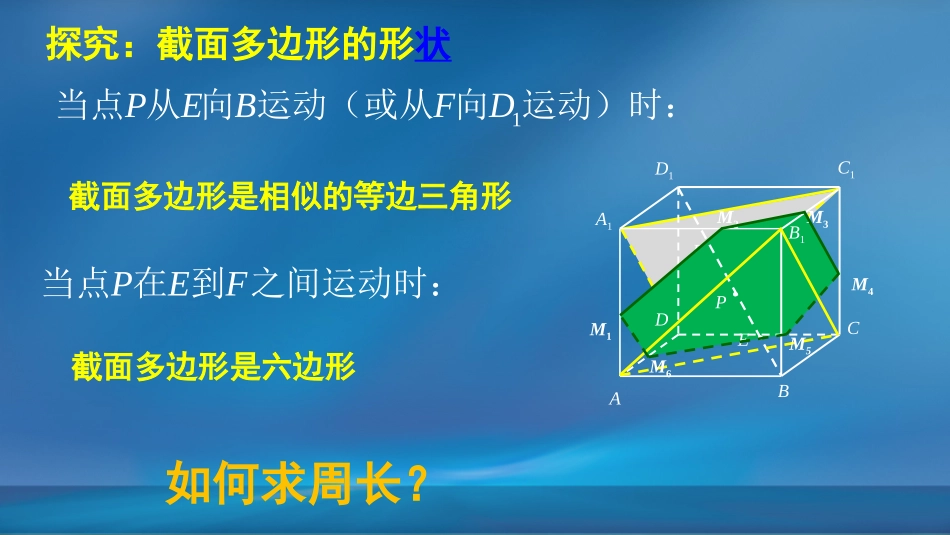
立体几何中的最值问题（二）主讲人曹永芹北京市第十七中学周长的最值童嘉森特级教师工作室111111-231,5()ABCDABCDPBDPBDyBPxxyfx如图：正方体的棱长为，动点在对角线上，过点作垂直于的平面，记这样得到的截面多边形（含三角形）的周长为，设，则当时，求函数的值域要求截面多边形的周长，关键是要找到符合要求的截面多边形.如何找？A1BC1C．ADB1D1．PNQTFA1BC1CADD1．B1PE如何求周长？1PEBFD当点从向运动（或从向运动）时：截面多边形是相似的等边三角形PEF当点在到之间运动时：截面多边形是六边形探究：截面多边形的形状．M1M2M3M4M6M511BPBMABBD11626BPxBDBA，，62BMx1AC正方体36x截面三角形周长等于136x当时，截面周长最小为()66PEF当运动到或时，周长最大为1,BDNQTPMNQT平面平面1BDPM探究：截面多边形周长的取值范围1.等边三角形的周长∽11RtBPMRtBADA1BC1C．ADB1D1．PMNQT2.截面六边形的周长166PBD观察发现：当运动到中点时，截面变为正六边形，很容易求出周长为猜想：是不是所有的六边形周长都等于？66探究：截面多边形周长的取值范围A1BC1C．ADB1D1．PNQT思路分析：由面面平行的性质定理得：111////EFACFMAB，111111111BFAFEFFMACABABAB，1111111-ABCDABCDACAB又正方体，1111111AFFBEFFMACAB1126EFFMAC2626MNNPPQQE，同理可得：66所以截面六边形的周长总等于()36,66.fx综上：函数的值域为NMFEPQA1BC1C．ADB1D1．P方法点睛本节课按照由特殊到一般的研究思路，以问题为牵引，层层探究，步步深入，采用了通过合情推理得出猜想，最后到推理验证的研究方法,求出周长最值.同学们,再见!