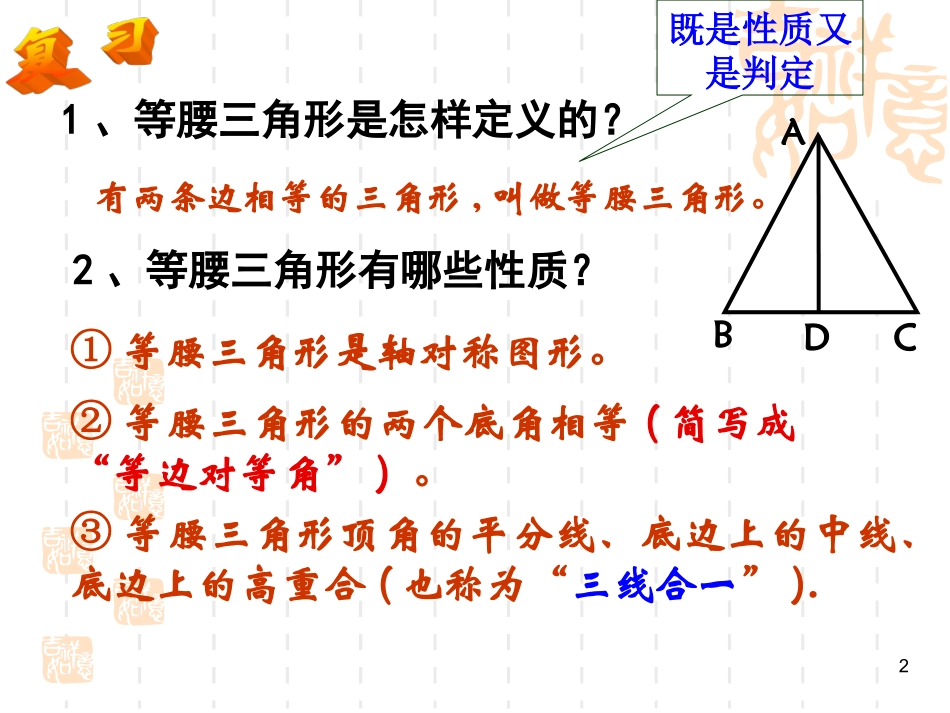
121、等腰三角形是怎样定义的?有两条边相等的三角形,叫做等腰三角形。①等腰三角形是轴对称图形。③等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”).②等腰三角形的两个底角相等(简写成“等边对等角”)。2、等腰三角形有哪些性质?DABC既是性质又是判定3把“等腰三角形的两个底角相等”改写成“如果------那么-----”形式。逆命题:如果一个三角形有两个角相等,那么这个三角形是等腰三角形.如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.它是真命题吗?4ABCD12已知:如图,在ΔABC中,∠B=∠C,求证:AB=AC。你还有其他证法吗?证明:过点A作∠BAC的平分线AD,交BC于点D,则∠1=∠2。在△BAD和△CAD中如果一个三角形有两个角相等,那么这两个角所对的边也相等。∠B=∠C∠1=∠2AD=AD(公共边)∴AB=AC(全等三角形的对应边相等)∴△BAD≌△CAD(AAS)5ABCD已知:如图,在ΔABC中,∠B=∠C,求证:AB=AC。证明:过点A作AD⊥BC,垂足为D.∴∠ADB=∠ADC(垂直的定义)在△ABD和△ACD中∠ADB=∠ADC∠B=∠CAD=AD(公共边)∴AB=AC(全等三角形的对应边相等)∴△ABDACD(AAS)≌△∵AD⊥BC6ABC如果一个三角形有两个角相等,那么这两个角所对的边也相等。几何语言:在△ABC中,∵∠B=∠C(已知)∴AB=AC(等角对等边)等腰三角形的判定定理:(简写成“等角对等边”)注意:在同一个三角形中应用哟!71.下列两个图形是否是等腰三角形?750300400400巩固练习:75°2在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是()A.∠A=50°,∠B=70°B.∠A=70°,∠B=40°C.∠A=30°,∠B=90°D.∠A=80°,∠B=60°B9例1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。ABCDE12如图,∠CAE是⊿ABC的外角,∠1=∠2,AD∥BC。求证:已知:AB=AC。∵AD∥BC(已知)∴∠1=∠B(两直线平行,同位角相等)∠2=∠C(两直线平行,内错角相等)∵∠1=∠2(已知)∴∠B=∠C(等量代换)∴AB=AC(等角对等边)证明:10例2、如图,上午10时,一艘轮船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°,∠NBC=80°求从B处到灯塔C的距离。解:∵∠NBC=A+C,A=40°∠∠∠∴∠C=∠NBC-A=80°-40°=40°∠∴∠C=A∠∴BA=BC(等角对等边)∵AB=20×(12-10)=40(海里)∴BC=AB=40(海里)答:从B处到达灯塔C的距离为40海里。80°40°NBAC北11BADC已知:如图,AD∥BC,BD平分∠ABC,求证:AB=AD.证明:∵AD∥BC∴∠ADB=∠DBC∵BD平分∠ABC∴∠ABD=∠DBC∴∠ABD=∠ADB∴AB=AD12如图:在△ABC中,已知D为BC边的中点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF,那么AB=AC吗?解:AB=AC;理由:∵点D为BC边的中点,∴DB=DC,∵DEAB⊥于点E,DFAC⊥于点F,∴△DEB和△DFC为直角三角形。在Rt△DEB和Rt△DFC中,DE=DFDB=DC∴RtDEBDFC△≌△(HL)∴∠B=C∠(全等三角形的对应角相等)∴AB=AC(等角对等边)13思考:若添加一个条件,使得△ABC是等边三角形,不再添加字母和线段,看你能说出多少个不同的添加。如图:在△ABC中,已知D为BC边的中点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF,那么AB=AC吗?14课堂小结名称图形概念性质判定等腰三角形ABC有两边相等的三角形是等腰三角形等边对等角三线合一轴对称图形等角对等边两边相等两腰相等作业教材第84页练习第1题第2题习题13.3第5题第6题