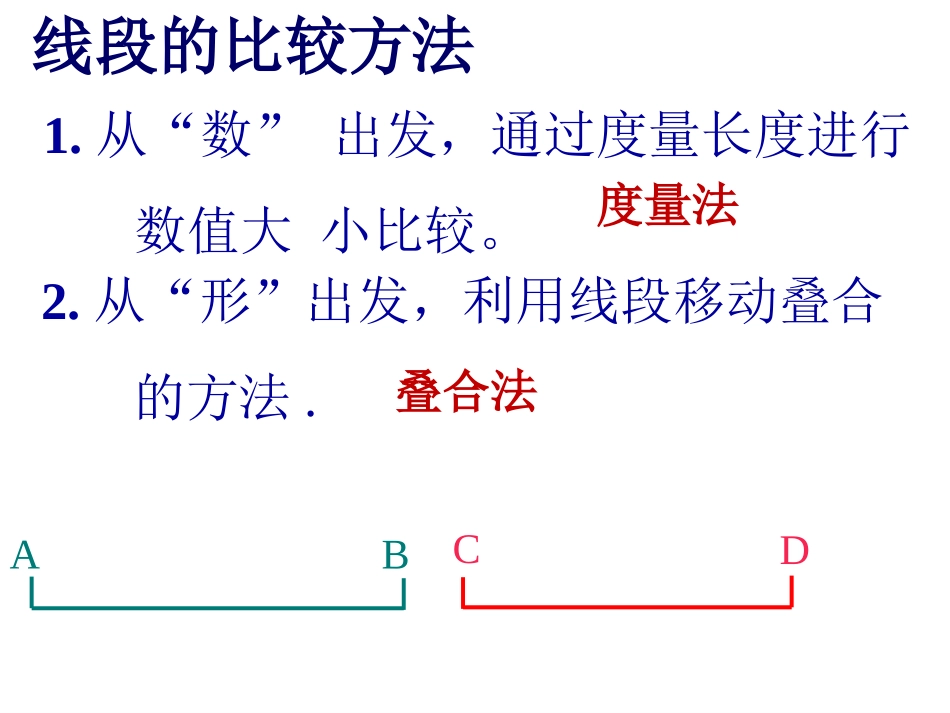
线段的比较方法2.从“形”出发,利用线段移动叠合的方法.ABCD1.从“数”出发,通过度量长度进行数值大小比较。度量法叠合法45°60°AoBDEF所以:∠AOB<∠DEF读数为45读数为60一、如何比较角的大小?ED落在∠ABC的外部,则∠DEF>∠ABC。把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。ABCDEF()()比较∠ABC和∠DEF的大小()()()例如:ED与BA重合,则∠DEF=∠ABC。把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。ABCDEF比较∠ABC和∠DEF的大小例如:ED落在∠ABC的内部,则∠DEF<∠ABC把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。ABCDEF()()比较∠ABC和∠DEF的大小1OAB2CBOA1BOOBC2顶点与一边重合二、角的和差运算1OAB2CBOA1BOOBC2AOC为1与2的和记作AOC=1+2()AOC为1与2的差记作AOC=1–2()顶点与一边重合二、角的和差运算OACB思考:下图中共有几个角?它们有什么关系?完成下列问题:1、图中共有__个角,它们分别是______________2、∠AOB=____+_____3、∠AOC=____-_____4、∠BOC=____-_____3∠AOBAOCBOC∠∠∠AOCBOC∠∠AOBBOC∠∠AOBAOC∠1、按图填空:2)∠A0B+∠BOC=3)∠A0C+∠COD=4)∠B0D-∠COD=∠A0D-=∠A0BODCBA∠AOC∠AOD∠BOC∠BOD1)∠D0B∠BOC∠C0B∠AOC∠D0C+∠COBB0D∠><=例1如图,O是直线AB上一点,∠AOC=53°17′,求∠BOC的度数.BOCA2、巩固应用,深入理解ABDC观察一副三角板的角度特征,讨论用三角板可以组合画出多少个不同角度的角.三、实践活动,探索新知利用一副三角板可以组合画出15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°,180°的角.2121BOACO当1=2时,射线OB把AOC分成两个相等的角,这时OB叫做AOC的平分线,也可以说OB平分AOC定义:在角的内部,自顶点引一条射线把这个角分成两个相等的角,那么,这条射线叫做角的平分线。符号表达:AOC∵OB是的角平分线∴,12AOBBOCAOC22AOCAOBBOC角的三等分线ααααααα角的四等分线ABCDO四、角的平分线问题4.如何作一个角的平分线?你能想到什么方法?度量法折纸法五、合作交流,探索新知例1、如图,已知∠AOB=90°,∠BOC=60°,OD是∠AOC的平分线,求∠BOD的度数.CABDO六、巩固新知ABCDE2、已知:如图,AD、BE分别是∠BAC和∠ABC的角平分线,且∠BAD=41°,∠ABC=80°.求:∠DAC、∠BAC、∠EBC的度数.例2.如图,已知∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,求∠DOE.OBADEC解:∵∠AOB=90°∠AOC=60°,∴∠BOC=∠AOB+∠AOC=90°+60°=150°,∵OD平分∠BOC,∴∠BOD=∠DOC=∠BOC=75°21∵OE平分∠AOC,∠AOC=60°∴∠AOE=∠EOC=∠AOC=30°21∴∠DOE=∠DOC-∠COE=75°-30°=45°答:∠DOE的度数是45°.∴∠AOE=∠EOC=∠AOC=30°213.如图,已知∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,求∠DOE.OBADEC(2)在上题中,若∠AOC是任意一个锐角,其他条件不变,你还能求出∠DOE的度数吗?说出你的理由.练习(1)如果∠AOB=130°,那么∠COE=°;(2)如果∠AOB=90°,那么∠COE=°;(3)如果∠AOB=°,那么∠COE=°;如图,OC是∠AOD的角平分线,OE是∠DOB的角平分线.OBACDE65452(4)如果∠AOB=130°,∠COD=20°那么∠BOE=°;45例2、如图,已知射线OD将∠AOB分成1:3两部分,射线OC将∠AOB分成5:7两部分,若∠COD=15°,求∠AOB的度数.CABDO六、巩固应用,深入理解例2把一个周角7等分,每一份是多少度的角(精确到分)?巩固应用,深入理解通过这堂课的学习,你有什么收获?1、比较两个角大小的方法2、角的和、差、倍、分关系3、角平分线把一个周角7等分,每一份是多少度的角?(精确到分)解:360°÷7=51°+3°÷7=51°+180′÷7≈51°26′答:每份中的角应该是51°26′(精确到秒)