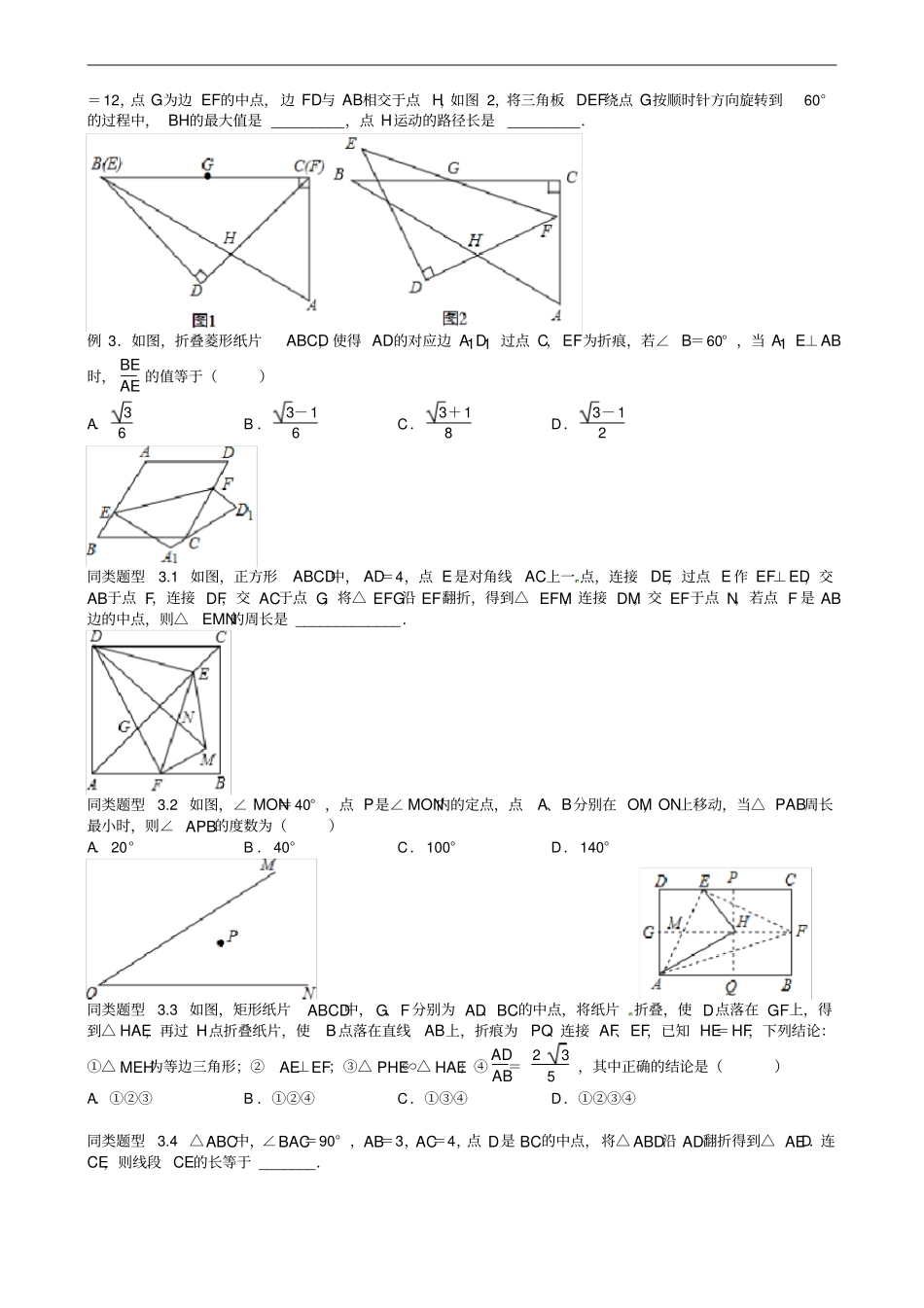
专题08几何变换问题例1.如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为______________.(结果保留根号)同类题型1.1把图中的一个三角形先横向平移x格,再纵向平移y格,就能与另一个三角形拼合成一个四边形,那么x+y()A.是一个确定的值B.有两个不同的值C.有三个不同的值D.有三个以上不同的值同类题型1.2已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为()A.S1>S2B.S1=S2C.S1<S2D.不能确定例2.如图,P是等边△ABC外一点,把BP绕点B顺时针旋转60°到BP′,已知∠AP′B=150°,P′A:P′C=2:3,则PB:P′A是()A.2:1B.2:1C.5:2D.3:1同类题型2.1如图,△ABC为等边三角形,以AB为边向形外作△ABD,使∠ADB=120°,再以点C为旋转中心把△CBD旋转到△CAE,则下列结论:①D、A、E三点共线;②DC平分∠BDA;③∠E=∠BAC;④DC=DB+DA,其中正确的有()A.1个B.2个C.3个D.4个同类题型2.2如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是12,其中正确结论的个数是()A.2B.3C.4D.5同类题型2.3在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,使点B在直线CD上,连接OD交AB于点M,直线CD的解析式为__________.同类题型2.4如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连结CE,CF,若∠CEF=α,∠CFE=β,则tanα﹒tanβ=___________.同类题型2.5如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.同类题型2.6如图1,一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12,点G为边EF的中点,边FD与AB相交于点H,如图2,将三角板DEF绕点G按顺时针方向旋转到60°的过程中,BH的最大值是_________,点H运动的路径长是_________.例3.如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,BEAE的值等于()A.36B.3-16C.3+18D.3-12同类题型3.1如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是_____________.同类题型3.2如图,∠MON=40°,点P是∠MON内的定点,点A、B分别在OM,ON上移动,当△PAB周长最小时,则∠APB的度数为()A.20°B.40°C.100°D.140°同类题型3.3如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE,再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF,已知HE=HF,下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④ADAB=235,其中正确的结论是()A.①②③B.①②④C.①③④D.①②③④同类题型3.4△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED.连CE,则线段CE的长等于_______.专题08几何变换问题例1.如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为______________.(结果保留根号)解:如图:连接B′B″, 在Rt△ABC中,AB=12,∠A=30°,∴BC=12AB=6,AC=63,∴B′C=6,∴AB′=AC-B′C=63-6, B′C∥B″C″,B′C=B″C″,∴四边形B″C″CB′是矩形,∴B″B′∥BC,B″B′=C″C,∴△AB...