三角形与多边形的内角和VIP免费

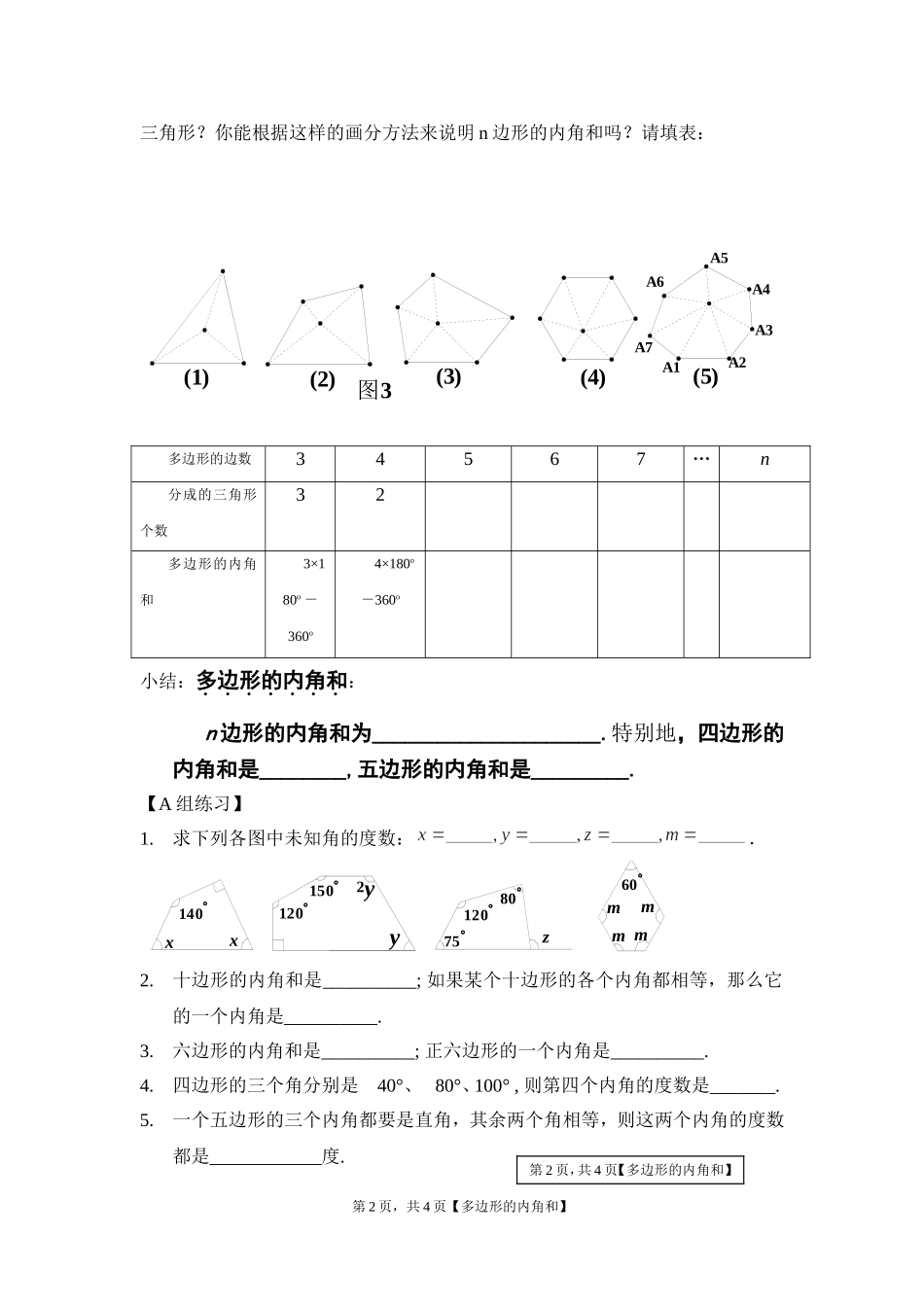
三角形与多边形的内角和姓名__________学号____【学习目标】1．理解多边形内角和的推导方法-----转化为三角形内角和问题．2．能运用多边形内角和定理进行简单说理和计算．【新课】1.三角形的定义：由________条不在同一直线上的线段首尾顺次连结组成的图形称为三角形.2.多边形的定义：由________条不在同一直线上的线段_______________组成的图形称为________形．3.图1（1）中的三角形记作_______________;图1（2）中的四边形记作;图1（3）中的五边形记作_______________;图1（4）中的六边形记作_______________.(2)(3)(4)图1(1)DCBAFABCABCDDEABCE4.正多边形的定义：如果多边形的各边都___________,各内角也都__________,那么就称它为正多边形.如图1(4)中的六边形就是_____________.5.多边形的对角线：连结多边形_________的两个顶点的线段叫做多边形的对角线.6.多边形的内角和：(1)如图2，从多边形的一个顶点引出的对角线把多边形划分为若干个三角形请填下表并找出规律，求多边形的内角和.(5)(1)图2(4)(3)(2)A6A5A7A1A2A3A4多边形的边数34567…n分成的三角形个数12多边形的内角和180o2×180o(2)如图3,在n边形内任取一点P,连结点P与多边形的每一个顶点，可得多少个第1页，共4页【多边形的内角和】第1页，共4页【多边形的内角和】三角形？你能根据这样的画分方法来说明n边形的内角和吗？请填表：(2)(3)(4)图3(1)(5)A4A3A2A1A7A5A6多边形的边数34567…n分成的三角形个数32多边形的内角和3×180o－360o4×180o－360o小结：多边形的内角和：n边形的内角和为_____________________.特别地，四边形的内角和是________,五边形的内角和是_________.【A组练习】1.求下列各图中未知角的度数：．140xxy1201502yz801207560mmmm2.十边形的内角和是__________;如果某个十边形的各个内角都相等，那么它的一个内角是__________.3.六边形的内角和是__________;正六边形的一个内角是__________.4.四边形的三个角分别是40°、80°、100°,则第四个内角的度数是_______.5.一个五边形的三个内角都要是直角，其余两个角相等，则这两个内角的度数都是____________度.第2页，共4页【多边形的内角和】第2页，共4页【多边形的内角和】6.已知一个多边形的内角和是2340o,求这个多边形的边数。7.一个三角形的三角内角的比分别是1：2：3，求这个三角形各内角的度数。【B组练习】8.一个四边形的四个内角的比分别是1：2：3：3，求这个四边形各内角的度数.9.一个n边形的每一个内角都等于140o,求n.10.辨析训练：(1)一个三角形中最多有个直角？为什么？(2)一个三角形中最多有个钝角？为什么？(3)一个三角形中至少有个锐角？为什么？(4)直角三角形的外角可以是锐角吗？为什么？11.求下列各图中∠1的度数。图(1)中，第3页，共4页【多边形的内角和】第3页，共4页【多边形的内角和】∠1=_______;图(2)中，∠1=_______;图(3)中，∠1=_______；图(4)中，∠1=_______;图(5)中，∠1=_______.(1)(2)(3)(4)(5)1654050111040110010013017030【C组练习】12.在一个多边形中，它的内角最多可以有______个是锐角。请说明理由。13.如果一个多边形的边数增加一条，那么它的内角和增加______________.请写出详细的解题过程.解n边形的内角和是___________,n+1边形的内角和是________.________________________________14.若一个多边形的对角线的条数恰好是边数的3倍，则这个多边形的边数是（）A.6B.7C.8D.915.从n边形的一个顶点出发，可以作________条对角线。n边形的对角线一共有____________条.小结：这一课我学会的知识有：第4页，共4页【多边形的内角和】第4页，共4页【多边形的内角和】