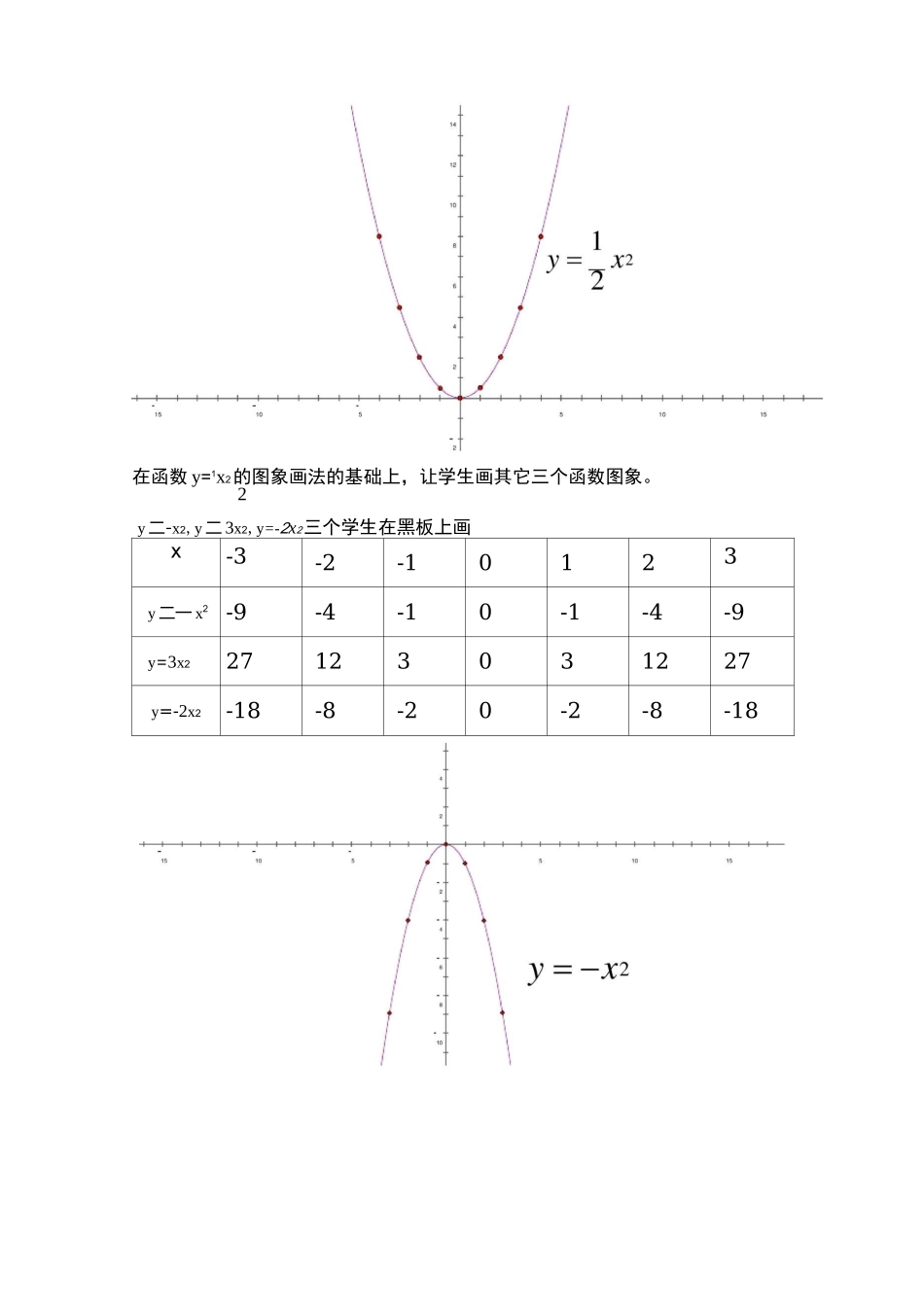
二次函数y=ax2'a丰0的图象和性质教案教学目标:知识与技能:绘画出二次函数的图象,知道二次函数的图象是抛物线,根据图象掌握性质。过程与方法:经历列表,描点,连线画出二次函数图象的过程体会观察数形结合从特殊到一般,分类等数学方法在探究二次函数图象和性质中的作用。情感态度与价值观:培养学生动手画函数图象,观察图象独立思考的能力,提高学生学习数学的兴趣。教学重难点教学重点:画二次函数图象,领悟二次函数的过程教学难点:数形结合发现二次函数性质课型,课时:新课,一课时教学用具:有平面直角坐标系的方格纸,课本教学方法:观察法,讨论法,总结归纳法教学过程:一,复习引入同学们上节课我们初步认识了二次函数,那么谁愿意回答什么叫做二次函数?(几名学生回答完了,老师再进行总结)形如y二ax2+bx+c(a丰0)函数称为二次函数,(其中x是自变量,a,b,c是常数)接下来需要进一步研究关于二次函数的什么内容呢?请同学们打开课本29页,看下方1二一x2,y=-x2,y=3x222.1.2二次函数y=ax2\a丰0丿的图象和性质(老师板书)同学们想一想,如何画二次函数的图象呢?回顾一下我们是否学过别的函数?让学生自由回答,学过一次函数,画图时(列表,描点,连线)类比一次函数,我们一起来画一下二次函数的图象。二,给几个特殊的二次函数画图让学生说一说,你想画哪一个二次函数图象,学生答案是各种各样的,也有简单的也有复杂的,举7-8个1y=_x2,y=-x2,y=3x2,y=3x2-6x+1,y=2x2-1,y=-5x2+x,y=-2x2(答案不唯一)同学们我们都知道认识事物时从简单到复杂。学习二次函数图象的初步先画四个简单的二次函数的图象(列表,描点,连线)从中我们选简单的函数y=ax2(a丰0)老师跟学生一起画函数y=x2的图象(老师示范)2x-4-3-2-1012341y=—x289210129822222在函数y=1x2的图象画法的基础上,让学生画其它三个函数图象。2y二-x2,y二3x2,y=-2x2三个学生在黑板上画x-3-2-10123y二一x2-9-4-10-1-4-9y=3x227123031227y=-2x2-18-8-20-2-8-18同学们观察四个二次函数图象发现了有哪些相同点和不同点?①相同点:形状相同,过原点,曲线,关于y轴对称(学生回答)虽然这些图象都过原点但后面的学习当中会发现有些二次函数图象不过原点,今天我们学习的是比较特殊的二次函数。我们看出来了,这四个图象跟一次函数图象不一样,很像一个物体抛出后落下来的轨迹,所以把这个曲线称为抛物线。二次函数图结论:二次函数图象抛物线>0,开口向上从图中可以看出二次函数y=12x2,y=―x2开口大小比较大,象具有对称性,关于一条直线对称的,从图中可以看出这四个图象关于y轴对称,后面学习复杂的二次函数图象不一定关于y轴对称,但他们关于一条直线对称的,后面我们继续学习。②不同点:开口方向不同,开口大小也不同1二次函数y=x2,y=3x2图象抛物线开口向上2二次函数y=-2x2,y=-x2图象抛物线开口向下③为什么有的抛物线开口向上,有的向下跟什么有关?y=1x2,y=3x2开口向上a>0(a是二次项系数)2y=-2x2,y=-x2开口向下a<0(0是二次项系数)y=3x2,y=-2x2开口大小比较小,这跟二次项系数a的绝对值有关,越大开口越小,越小开口越大。④一次函数图象有些上升,有些下降的,同样我们看一下二次函数图象上升,下降情况。从图中可知这四个二次函数图象都是对称轴y轴左右边上升,下降。当a>0时,y轴右侧上升,左侧下降当a<0时,y轴右侧下降,左侧上升四,总结同学们本节课你有什么收获?y=ax2(a>0)y=ax2(a<0)图象抛物线抛物线开口向上向下对称轴y轴y轴顶点原点(0,0)原点(0,0)开口大小a越大开口越小,艸越小开口越大增减性对称轴右侧y随x的增大而增大,对称轴左侧y随x的增大而减小。对称轴右侧y随x的增大而减小,对称轴左侧y随x的增大而增大。布置作业:课本32页练习及练习册相关内容板书设计:二次函数y=ax2(a丰0)的图象和性质x-4-3-2-1012341y=—x289210129822222y二1x22教学反思: