【全程复习方略】2013版高中数学-6.5合情推理与演绎推理配套课件-苏教版VIP专享VIP免费

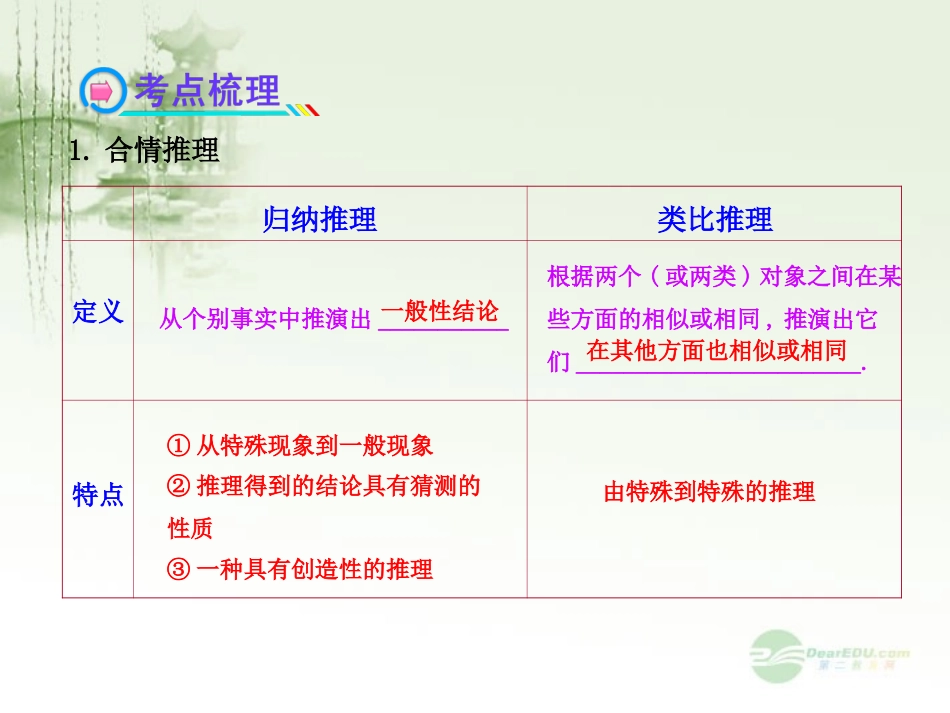
第五节合情推理与演绎推理内容要求ABC合情推理与演绎推理√…………三年2考高考指数:★★★1.合情推理类比推理归纳推理定义特点从个别事实中推演出___________根据两个(或两类)对象之间在某些方面的相似或相同,推演出它们________________________.①从特殊现象到一般现象由特殊到特殊的推理一般性结论在其他方面也相似或相同②推理得到的结论具有猜测的性质③一种具有创造性的推理2.合情推理的解题流程(1)归纳推理实验、观察→概括、推广→猜测一般性结论(2)类比推理观察、比较→联想、类推→猜测新的结论【即时应用】(1)判断下列命题是否正确.(请在括号中填“√”或“×”)①(ab)n=anbn与(a+b)n类比，则有(a+b)n=an+bn;()②loga(xy)=logax+logay与sin(α+β)类比，则有sin(α+β)=sinαsinβ;()③(a+b)2=a2+2ab+b2与(+)2类比，则有(+)2=.()(2)数列2,5,11,20,x,47,…中的x等于______.arbrarbr22a2abb【解析】(1)①错.(a+b)2=a2+2ab+b2≠a2+b2;②错.sin(α+β)=sinαcosβ+cosαsinβ≠sinαsinβ;③对.(+)2=(+)·(+)=满足向量数量积的运算.(2)5-2=3,11-5=6,20-11=9,推出x-20=12，所以x=32.答案：(1)①×②×③√(2)32arbrarbrarbr22a2abb3.演绎推理(1)定义：演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等)，按照_______________得到新结论的推理过程.(2)模式：(3)特点：由一般到特殊的推理(4)格式：M-P(M是P)S-M(S是M)S-P(S是P)①大前提——三段论②小前提——特殊对象③结论——一般原理与特殊对象间的内在联系严格的逻辑法则一般性的原理【即时应用】(1)命题“有些有理数是无限循环小数，整数是有理数，所以整数是无限循环小数”是假命题，判断下列说法的真假(填“真”，“假”)①使用了归纳推理()②使用了类比推理()③使用了演绎推理()④使用了“三段论”但推理形式错误()⑤使用了“三段论”但小前提错误()(2)判断下列推理过程是否是演绎推理(请在括号中填“是”或“否”)①两条直线平行，同旁内角互补，如果∠A和∠B是两条平行直线的同旁内角，则∠A+∠B=180°()②某校高三(1)班有55人，(2)班有54人，(3)班有52人，由此得高三所有班级人数超过50人()③由平面三角形的性质，推测空间四边形的性质()④在数列{an}中，a1=1,an=(an-1+)(n≥2,n∈N*)，由此归纳出{an}的通项公式()12n11a【解析】(1)①假：不满足归纳推理的定义；②假：不满足类比推理的定义；③真：满足演绎推理的定义；④真：使用了“三段论”但大前提中的“有些有理数”与小前提中的“有理数”不是同一概念，故不符合三段论的推理形式.⑤假，使用了“三段论”但小前提是正确的.(2)①是，使用了“三段论”.②不是，使用了归纳推理不是演绎推理.③不是，使用了类比推理.④不是,使用了归纳推理.答案：(1)①假②假③真④真⑤假(2)①是②否③否④否归纳推理【方法点睛】归纳推理的特点(1)归纳推理是由部分到整体，由个别到一般的推理.(2)归纳推理所得结论不一定正确，通常归纳的个体数目越多，越具有代表性，推广的一般性结论也会越可靠.(3)归纳推理是一种发现一般性规律的重要方法，其结论的正确性往往通过演绎推理来证明.【例1】(1)已知：f(x)=,设f1(x)=f(x),fn(x)=fn-1(fn-1(x))(n>1且n∈N*),则f3(x)的表达式为______，猜想fn(x)(n∈N*)的表达式为______.(2)(2012·苏州模拟)观察式子：你可以猜出的一个一般性结论是________.(3)设f(x)=，先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3)，然后归纳猜想一般性结论，并给出证明.x1x11358791127x133【解题指南】(1)由已知条件及递推关系可推得f2(x),f3(x)及fn(x).(2)由三个等式可推第四，第五个等式，从而得第n个等式即一般结论.(3)由0+1=1,-1+2=1,-2+3=1,而x+(1-x)=1猜想f(x)+f(1-x)可证.【规范解答】(1)由f1(x)=f(x)=得f2(x)=f1(f1(x))=f1()=f3(x)=f2(f2(x))=f2()=f4(x)=f3(f3(x))=f3()=故猜想fn(x)=答案：f3(x)=fn(x)=x1xx1xxx1x,x12x11xx12xx12xx1212x2xx14x12xx14xx14xx1414x3xx,18x12xn1...