必修2圆与圆的位置关系VIP免费

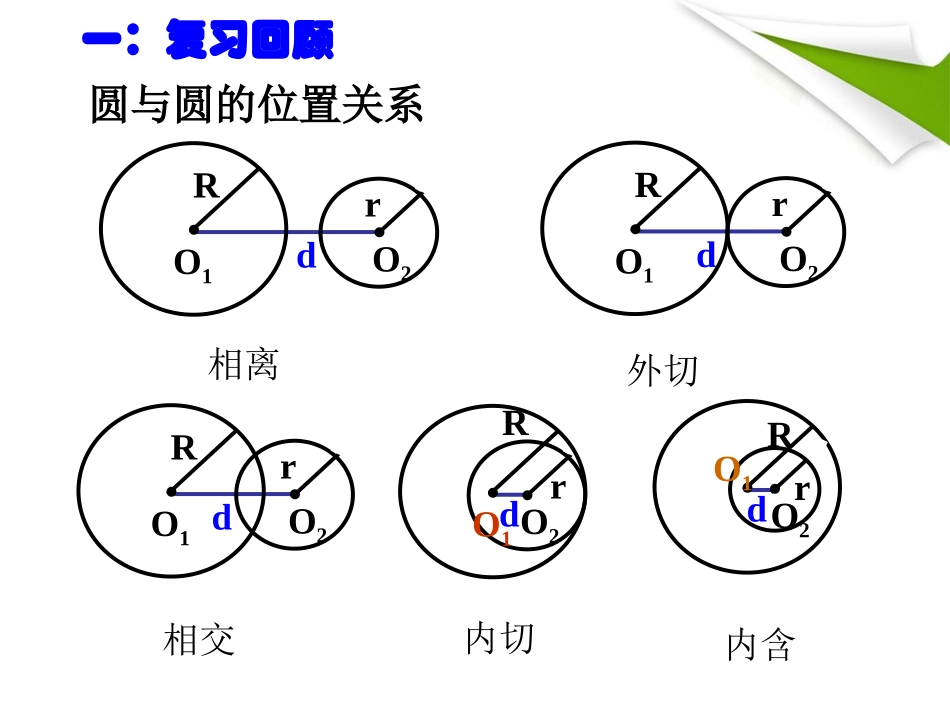
圆与圆的位置关系圆与圆的位置关系日全食•Rd•O2rO1•O2rd•O1R•O1R•O2rd•O1R•O2rd•O1R•O2rd相离外切相交内切内含圆与圆的位置关系一：复习回顾判断下列两圆的位置关系。与1)1()2(:221yxC16)5()2(:222yxC①②与076:221xyxC0276:222yyxC二、自主探究：•例1.已知圆1:C222880xyxy，2:C224420xyxy，试判断圆与圆的关系.圆1C2C三、典型例题分析：方法一，圆C1与圆C2有几个公共点，由它们的方程组成的方程组有几组实数解确定；方法二，可以依据连心线的长与两个半径长的和12rr或两半径长的差的绝对值12rr的大小关系，判断两圆的位置关系。解法一：222228804420xyxyxyxy210xy，圆与圆的方程联立，得到方程组1C2C-,得由，得12xy，把上式代入，并整理，得2230.xx方程的根的判别式2(2)41(3)160，所以，方程有两个不相等的实数根12xx，，把12xx，分别代入方程，得到12.yy，因此圆与圆1C2C有两个不同的公共点1122()().AxyBxy，，，•解法二：把圆的方程化为标准方程，得1C22(1)(4)25.xy圆1C的圆心是点(1,4),半径长15.r把圆的方程化为标准方程，得22(2)(2)10.xy2C圆2C的圆心是点(2,2),半径长210.r圆1C与圆2C的连心线的长为22(12)(42)35，2C12510rr，圆1C与圆2C的两半径之差是12510rr，而51035510即1212310rrrr，圆1C与圆的两半径之和是所以圆的两半径之差是1C与圆2C相交，它们有两个公共点Ａ，Ｂ.1C公共弦例2.已知圆:1C016222yxyx:2C与圆.0112422yxyx求两圆的公共弦所在的直线方程及公共弦长。例3.经过A(4,4)向圆(x+2)2+(y+2)2=8作两条切线，切点分别为A，B，求经过A，B两点的直线方程。练习：已知圆C1：x2+y2－2mx+m2=4和圆C2：x2+y2+2x－4my=8－4m2相交，求实数m的取值范围.122(,)(0,2)55m本节课学习了圆与圆的位置关系，有代数法和几何法。几何法：直观容易理解，但不能求出交点坐标。代数法：只能判断交点，不能准确判断关系，如外切与内切不能区分。优点是可以求出公共点。四、课堂小结：五、布置作业(一)课本习题4.2A组10,11；B组5。(二)课外思考1、课本P130练习中两圆有多少条公切线？2、已知A(-1,2),B(2,6),问存在多少条直线l使A,B到l的距离分别为2和3？