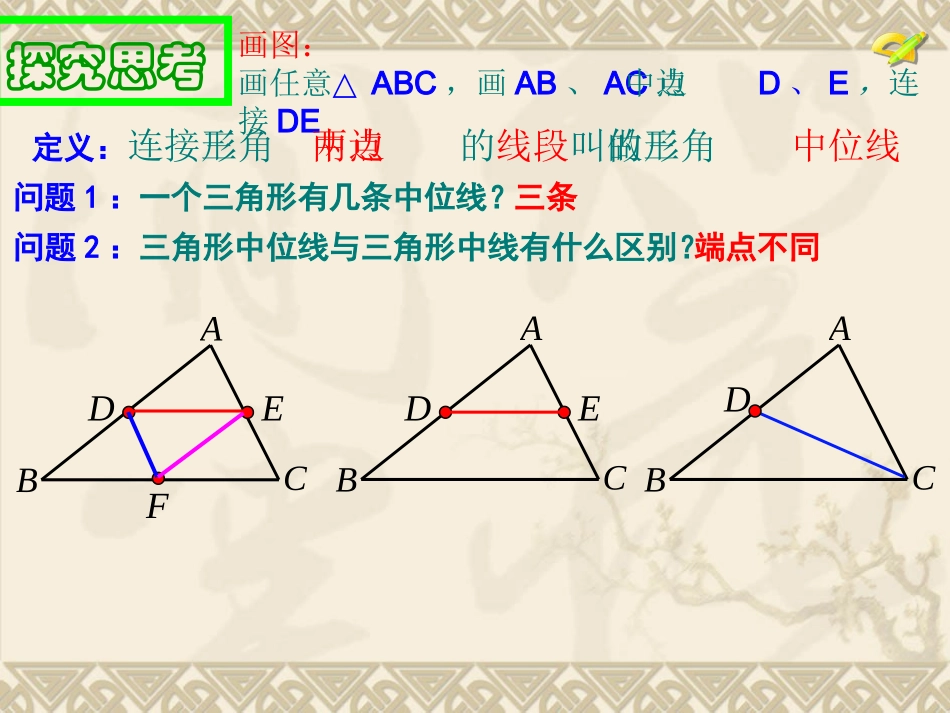
zx``xk18.1.218.1.2平行四边形的判定平行四边形的判定第第33课时课时温故知新平行四边形的判定边角对角线两组对边分别平行的四边形是平行四边形一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形探究思考画图:画任意△ABC,画AB、AC边中点D、E,连接DEABCDE定义:连接三角形两边中点的线段叫做三角形的中位线问题1:一个三角形有几条中位线?三条问题2:三角形中位线与三角形中线有什么区别?端点不同FABCABCDED探究思考问题3:如图,DE是△ABC的中位线,DE与BC有怎样的关系?ABCDE两条线段的关系位置关系数量关系分析:DE与BC的关系猜想:DE∥BC?12DEBC猜想:三角形的中位线平行于第三边且等于第三边的一半.探究思考证明:ABCDE延长DE到F,使EF=DE连接AF、CF、DC.∵AE=EC,DE=EF,∴四边形ADCF是平行四边形.F∴四边形BCFD是平行四边形证法1:∴CFAD//∴CFBD//12DEDF又∵∴DE∥BC,12DEBC∴DFBC//已知:D、E分别是△ABC的边AB、AC的中点.求证:DE∥BC,12DEBCABCDE探究思考证明:延长DE到F,使EF=DE.连接FCF∴四边形BCFD是平行四边形.∴△ADE≌△CFE.∴∠ADE=∠F,AD=CF证法2:∴AB∥CF又∵AD=BD.∴BD=CF12DEDF又∵∴DE∥BC,12DEBC∴DFBC//在△ADE和△CFE.ECAECEFAEDFEDE探究思考三角形的中位线平行于三角形的第三边且等于第三边的一半∵△ABC中,若D、E分别是边AB、AC的中点∴DE∥BC,DE=BC12三角形中位线定理:符号语言:ABCDE或:∵AD=BD、AE=CE∴DE∥BC,DE=BC12学以致用1.如图,△ABC中,D、E分别是AB、AC中点.(1)若DE=5,则BC=.(2)若∠B=65°,则∠ADE=.(3)若DE+BC=12,则BC=.ABCDE1065°82.在△ABC中,AB=10,AC=6,BC=8且D、E、F分别是AB、AC、BC的中点,求△DEF的周长和面积.ACBEDF学以致用例在四边形ABCD中E、F、G、H分别是AB、BC、CD、DA中点.求证:四边形EFGH是平行四边形.EGFHBCDA:三角形的中位线平行于三角形的第三边且等于第三边的一半∵△ABC中,若D、E分别是边AB、AC的中点∴DE∥BC,DE=BC12ABCDE或:∵AD=BD、AE=CE∴DE∥BC,DE=BC12归纳小结:连接三角形两边中点的线段叫做三角形的中位线三角形的中位线三角形的中位线定理