向量减法运算及其几何意义VIP免费

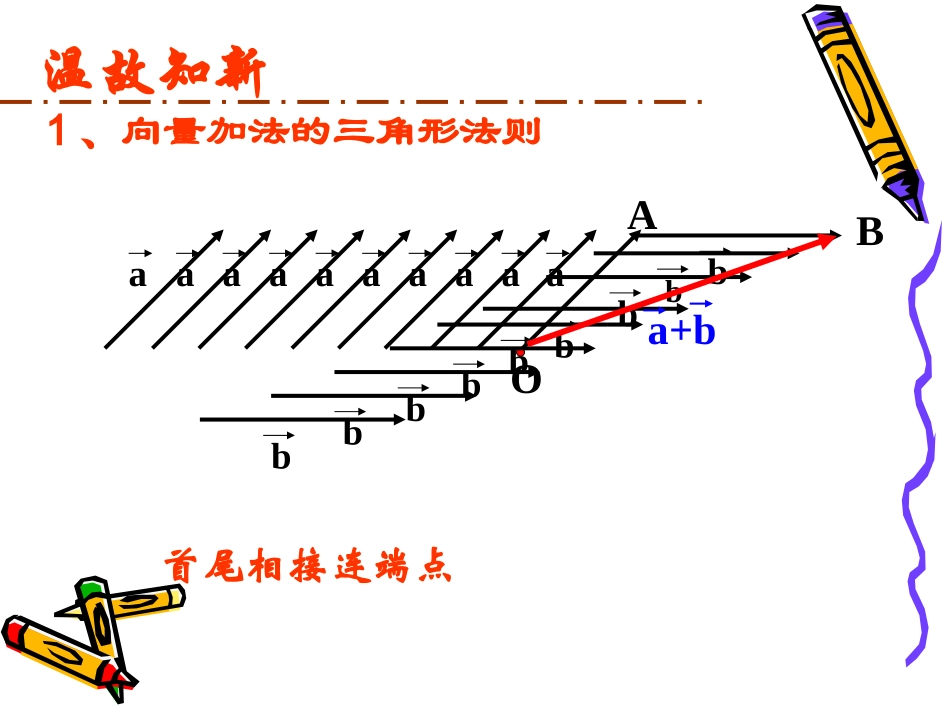
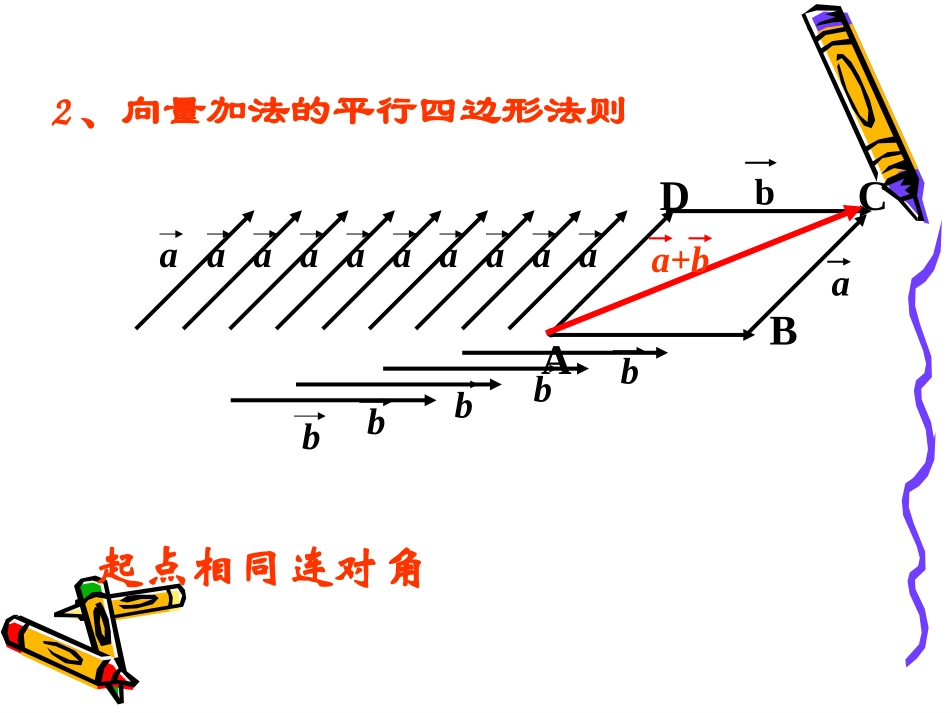
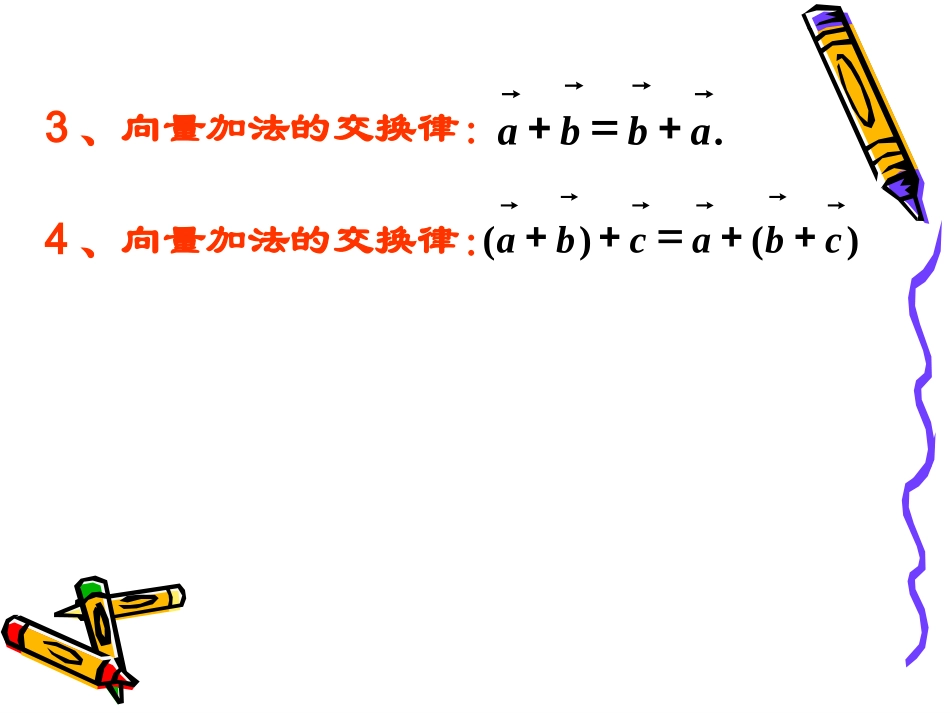1、向量加法的三角形法则baOaaaaaaaabbbbbbbBbaAa+b首尾相接连端点温故知新baAaaaaaaaabbbBbaDaCba+b2、向量加法的平行四边形法则起点相同连对角.abba)()(cbacba3、向量加法的交换律：4、向量加法的交换律：2.2平面向量线性运算2.2平面向量线性运算2.2.2向量减法运算及其几何意义探究向量是否有减法?如何理解向量的减法?我们知道,减去一个数等于加上这个数的相反数，如:5-1=5+(-1)向量的减法是否也有类似的法则：减去一个向量等于加上这个向量的相反向量？一、相反向量a定义：与长度相等，方向相反的向量，叫做的相反向量，记作：aa结论：（1）)(a（2）零向量的相反向量仍是零向量,aaaa)()()3(（4）如果是a,b互为相反的向量，那么baba,,00a0ba0aa在计算中常用,BAAB二、向量减法：定义：)(baba即：减去一个向量相当于加上这个向量的相反向量。把也叫做与的差。与的差也是一个向量。baabab三、向量减法的作图方法：呢？如何作出根据减法的定义，已知baba,,ab)(baba,,,abab��已知根据减法的定义如何作出呢？abaOAbBDCb()ab()ab:ab的作图方法四、向量减法的几何意义:abaOAbBab①将两向量平移,使它们有相同的起点.②连接两向量的终点.③箭头的方向是指向“被减数”的终点.baab减向量的终点被减向量的终，这就是向量点减表示从指向的向量法的几何意义.abba表示与的和等于也可理解为：的向量.“共起点，连终点，指向被减向量”思考?？abb(1)如图，如果从a的终点到b的终点作向量，那么所得向量是什么？aabab、线则应样：若向量共，怎作出呢？思考abab（1）（2）OABABOabab同向反向abab、线则应样：若向量共，怎作出呢？思考abab（1）（2）OABABOabab||||||||||||||||ababababababba若，方向相反，若，方向相同，（或）||||||ababab若，不共线，则||||||||||任意向量，，有||abababab||||||||||任意向量，，有||abababab||||||||||任意向量，，有||abababab||||||||||任意向量，，有||abababab1.,,,,,.abcdabcd��例已知向量求作向量ababccddABCDO.,,,.2.,,,,.1:为所求则作作在平面上任取点作法dcDCbaBADCBAdODcOCbOBaOAO练习,,.abab��如图，已知求作abaaabbb（1）（2）（3）（4）abababABoABoABoABBAOAOBab�oabab例2：选择题：()()()()ABACDBAADBACCCDDDC��（2）()()()()ABBCADAADBCDCDBDDC��（1）DCDBACbabADaABABCD,,,,,.2表示向量用已知平行四边形例abABCD解：有向量加法的平行四边形法则，得ACab�;由向量的减法可得，.DBABADab�,,,,ABCDABaDAbOCcbcaOA����如图平行四边形例4：证明：ABCDabcOOABAOBABOBacbOBCBOCOCDAcb证明：abABCD变式训练一：当a,b满足什么条件时，a+b与ab垂直？_____________||||ab变式训练二：当a,b满足什么条件时，|a+b|=|ab|？_____________________ab和互相垂直baba变式训练三：a+b与ab可能是相等向量吗？___________________________________________不可能.因为平行四边形的两条对角线方向不同.abABCDO如图,中,你能用表示向量AB和AD吗?变式训练四ABCD�AO=,OB=b,a,ba解:AB=a+b;AD=a-b.练习1_____;______;______;______;______.ABADBABCBCBAODOAOAOB�����填空：DB�BA�AD�AC�CA�BAAB重要提示你能将减法运算转化为加法运算吗？(一)知识1．理解相反向量的概念2.理解向量减法的定义，3.正确熟练地掌握向量减法的三角形法则小结:(二)重点重点：向量减法的定义、向...