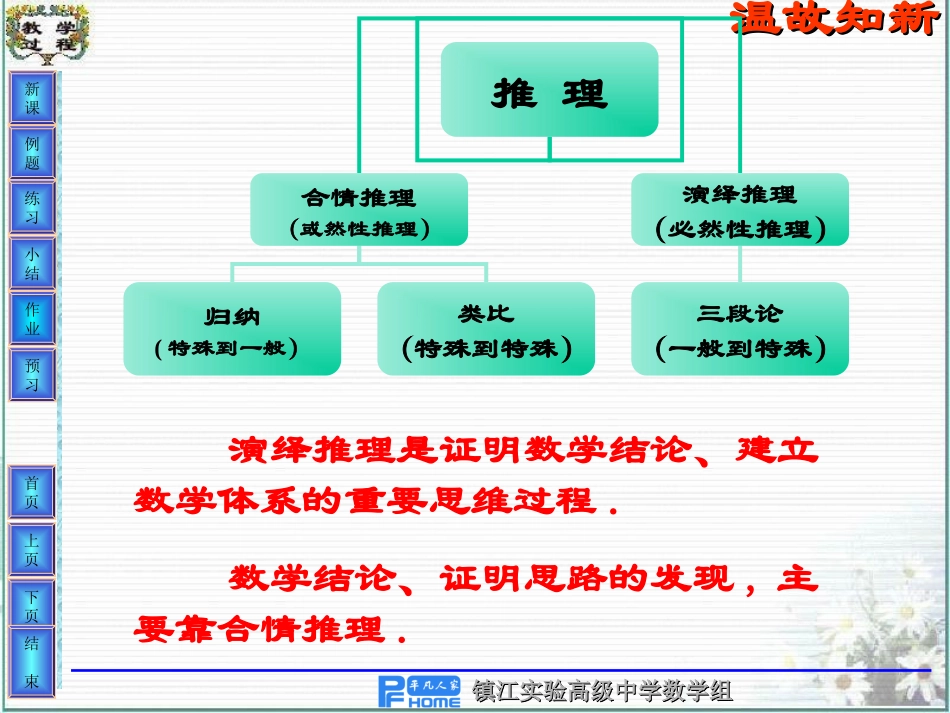
镇江实验高级中学数学组镇江实验高级中学数学组镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习温故知新温故知新演绎推理是证明数学结论、建立数学体系的重要思维过程.数学结论、证明思路的发现,主要靠合情推理.推理合情推理(或然性推理)演绎推理(必然性推理)归纳(特殊到一般)类比(特殊到特殊)三段论(一般到特殊)镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习探索求真探索求真试证明下列各题:试证明下列各题:11)等腰三角形两腰上的高相等;)等腰三角形两腰上的高相等;22)设)设aa、、bb是两个正实数,是两个正实数,求证:求证:abba2镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习利用已知条件和某些数学定义、公利用已知条件和某些数学定义、公理、定理等理、定理等,,经过一系列的推理论证经过一系列的推理论证,,最后推导出所要证明的结论成立最后推导出所要证明的结论成立,,这种这种证明方法叫做证明方法叫做综合法综合法。。((由因导果由因导果))用用PP表示已知条件、已有的定义、表示已知条件、已有的定义、公理、定理等公理、定理等,,QQ表示所要证明的结论表示所要证明的结论..则综合法用框图表示为则综合法用框图表示为::1PQ12QQ23QQnQQ…镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习例例11、、已知已知aa>0,>0,bb>0,>0,求证:求证:aa((bb22++cc22)+)+bb((cc22++aa22))≥≥44abcabc因为b2+c2≥2bc,a>0所以a(b2+c2)≥2abc.又因为c2+b2≥2bc,b>0所以b(c2+a2)≥2abc.因此a(b2+c2)+b(c2+a2)≥4abc.证明证明::实践出真知实践出真知镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习例例22、、已知已知aa,,bb,,cc为不全相等的正数,为不全相等的正数,求证:求证:3ccbabbacaacb例例33、、在在△△ABCABC中,三个内角中,三个内角AA、、BB、、CC对对应的边分别为应的边分别为aa、、bb、、cc,且,且AA、、BB、、CC成等成等差数列,差数列,aa、、bb、、cc成等比数列,求证△成等比数列,求证△ABABCC为等边三角形。为等边三角形。镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习能力展示能力展示1、设a、b是两个正实数,且a≠b,求证:a3+b3>a2b+ab233、课本、课本8181页第页第11,,22,,44题题2、设不等式mx2-2x-m+1<0对于满足|m|≤2的一切m的值都成立,求x的取值范围。镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习知识回顾知识回顾利用已知条件和某些数学定义、公利用已知条件和某些数学定义、公理、定理等理、定理等,,经过一系列的推理论证经过一系列的推理论证,,最后推导出所要证明的结论成立最后推导出所要证明的结论成立,,这种这种证明方法叫做证明方法叫做综合法综合法。。((由因导果由因导果))用用PP表示已知条件、已有的定义、表示已知条件、已有的定义、公理、定理等公理、定理等,,QQ表示所要证明的结论表示所要证明的结论..则综合法用框图表示为则综合法用框图表示为::1PQ12QQ23QQnQQ…镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习P84习题习题2.2–122、课本、课本8181页第页第11,,22,,44题题镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习先睹为快先睹为快例:在锐角三角形ABC中,求证:sinA+sinB+sinC>cosA+cosB+cosC镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习镇江实验高级中学数学组镇江实验高级中学数学组下页上页首页作业结束小结练习新课例题预习33、、设抛物线设抛物线yy22=2=2pxpx((pp>0)>0)的焦点为的焦点为FF,,经过点经过点FF的直线交抛物线于的直线交抛物线于AA、、BB两点,两点,点点CC在抛物线的准线上,且在抛物线的准线上,且BCBC∥∥xx轴轴((如图如图),),证明证明::直线直线ACAC经过原点经过原点OO。。42-2-4-65BACOF