_一次函数的图象课件VIP免费

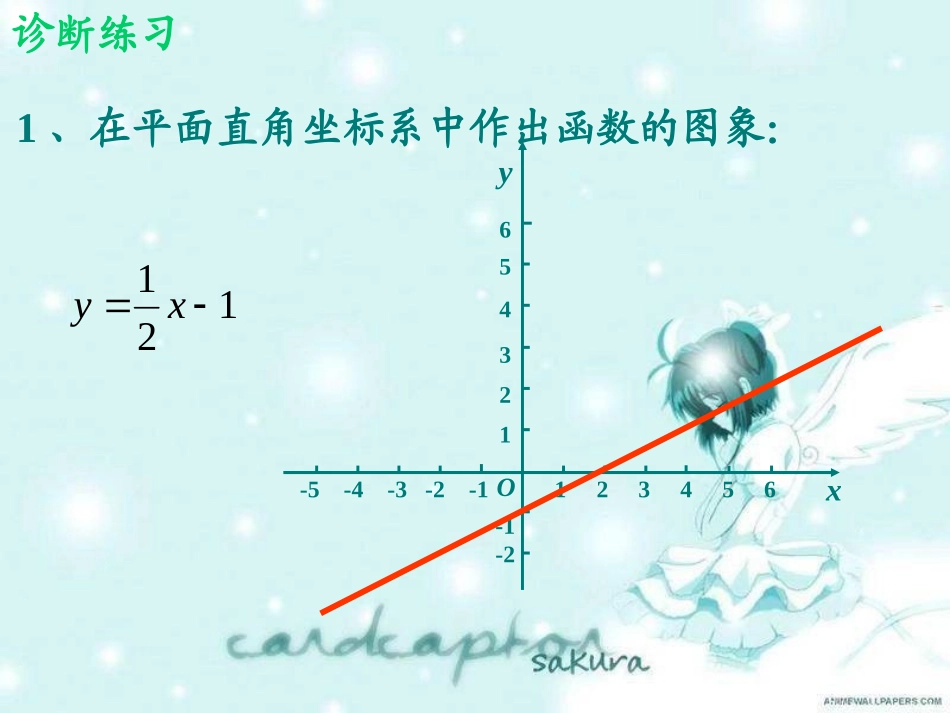
一次函数的图象一次函数的图象诊断练习1、在平面直角坐标系中作出函数的图象：121xyyxO-5-4-3-2-1123456654321-1-2复习旧知1、函数图象的定义：把一个函数的自变量x与对应的因变量y的值分别作为横坐标和纵坐标，在直角坐标系内描出它的对应点，所得这些点组成的图形叫做该函数的图象。复习旧知2、作函数图象的一般步骤：(1)列表：选择具有代表性的自变量的值和函数的对应值列成表格；(2)描点：将自变量的值作为横坐标,对应的函数值作为纵坐标,在坐标系中描出表格中的各点；(3)连线：按自变量从小到大的顺序，把所有点用平滑的曲线连接起来。复习旧知3、一次函数的图象：一次函数的图象是一条直线。bkxy4、一次函数图象的画法：用两点法画一次函数的图象。bkxy在同一直角坐标系内作出正比例函数的图象：情景引入;3)1(xy;)2(xy;2)3(xy.)4(xyyxO-5-4-3-2-11234554321-1-2-3-4-5xyxy3xy2xyyxO-5-4-3-2-11234554321-1-2-3-4-5xyxy3xy2xyⅠ、正比例函数的图象有什么特点？kxy图象经过原点新知探究新知归纳正比例函数的图象：正比例函数的图象是经过原点(0,0)的一条直线。kxykxyyxO-5-4-3-2-11234554321-1-2-3-4-5xyxy3xy2xyⅡ、你作正比例函数的图象时描了几个点？kxy新知探究(1,3)(1,1)(1,−2)(1,−1)(0,0)(1,k)作图时描了以下两点：Ⅲ、(1)以下两个函数中，随着x值的增大，y的值分别如何变化？新知探究yxO-5-4-3-2-11234554321-1-2-3-4-5xyxy3(2)哪条直线与x轴正方向所成的锐角最大？哪条直线与x轴正方向所成的锐角最小？随着x值的增大，y的值分别增大|k|越大，y值的增大得越快(3)直线在什么位置？k>0，直线过一、三象限新知归纳正比例函数的性质：(1)当k>0时，直线经过一、三象限，y的值随x值的增大而增大；kxyⅢ、(1)以下两个函数中，随着x值的增大，y的值分别如何变化？新知探究yxO-5-4-3-2-11234554321-1-2-3-4-5(2)哪条直线与x轴正方向所成的锐角最大？哪条直线与x轴正方向所成的锐角最小？随着x值的增大，y的值分别减小|k|越大，y值的减小得越快(3)直线在什么位置？k<0，直线过二、四象限xy2xy新知归纳正比例函数的性质：(1)当k>0时，直线经过一、三象限，y的值随x值的增大而增大；kxy(2)当k<0时，直线经过二、四象限，y的值随x值的增大而减小。1、函数中，y的值随x值的增大而。巩固练习34xy2、下列一次函数中，y的值随x值的增大而减小的有。巩固练习;910)1(xy;203)2(xy;45)3(xy.)32()4(xy合作交流ⅰ、在同一直角坐标系内分别作出一次函数的图象：;2)1(xy;32)2(xy.32)3(xyyxO-5-4-3-2-1123456654321-1-2-3-432xyxy2xy2合作交流ⅱ、(1)这三条直线有什么关系？yxO-5-4-3-2-1123456654321-1-2-3-432xyxy232xyk值相等，直线互相平行(2)这三条直线是通过怎样的变换而相互得到的？b>0，向上平移|b|个单位b<0，向下平移|b|个单位(3)这三条直线分别在什么位置？新知归纳一次函数的性质：(1)k>0，y的值随x值的增大而增大bkxy①b>0时，直线经过一、三、二象限；②b<0时，直线经过一、三、四象限。在同一直角坐标系内作出下列函数的图象：;131)1(xy;131)2(xy.31)3(xyyxO-5-4-3-2-1123456654321-1-2-3-4yxO-5-4-3-2-1123456654321-1-2-3-4xy31131xy131xy新知归纳一次函数的性质：(1)k>0，y的值随x值的增大而增大bkxy(2)当k<0时，y的值随x值的增大而减小①b>0时，直线经过一、三、二象限；②b<0时，直线经过一、三、四象限。①b>0时，直线经过二、四、一象限；②b<0时，直线经过二、四、三象限。一次函数与正比例函数的图象与性质一次函数y=kx+b（b≠0)图象k,b的符号经过象限增减性正比例函数y=kxxyobxyobxyobxyoby随x的增大而增大y随x的增大而增大y随x的增大而减少y随x的增大而减少一、二、三一、三、四一、二、四二、三、四１、图象是经过（０，０）与（１，k）的一条直线２、当k>0时，图象过一、三象限；y随x的增大而增大。当k<0时，图象过二、四象限；y随x的增大而减少。k>0b>0k>0b<0k<0b>0k<0b<04、x...