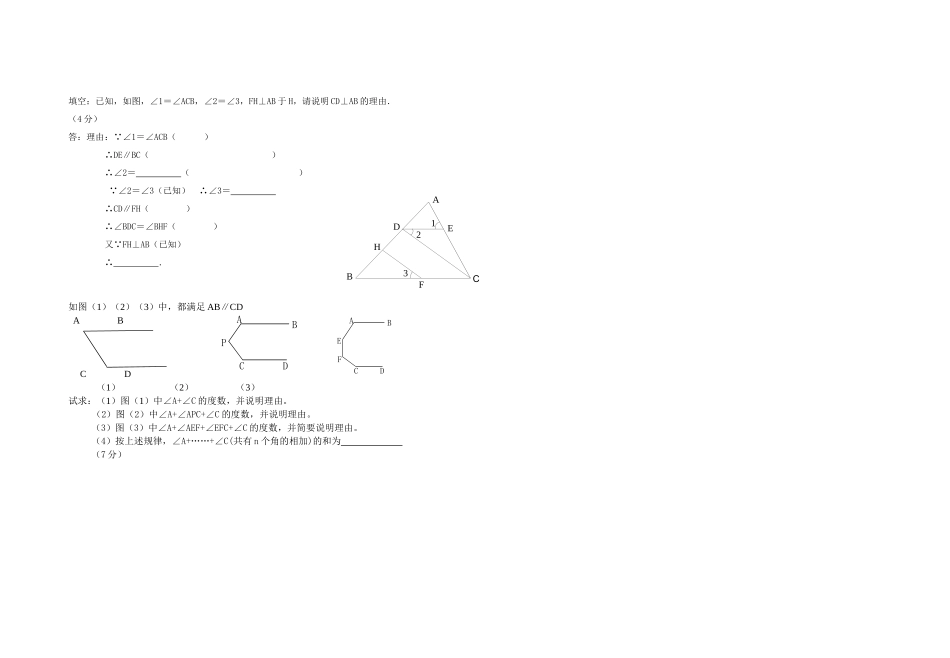
初一下学期第一次月考数学试卷一、选择题:(每题3分,共30分)1、如图所示,在的延长线上,下列条件中,能判断的是()A.B.C.D.2.如上图,直线l1l∥2,若∠1=140°,∠2=70°,则∠3的度数是()3下列各组数中,互为相反数的组是()A、-2与B、-2和C、-与2D、︱-2︱和24.列命题中,是真命题的是()A、同位角相等B、垂直于同一直线的两直线平行C、相等的角是对顶角D、平行于同一直线的两直线平行5在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,当∠AOC=30o时,∠BOD的度数是()A、60oB、120oC、60o或90oD、60o或120o‘6.-2,,,3.14,,,这6个数中,无理数共有()A、4个B、3个C、2个D、1个7对于实数a、b,给出以下三个判断:①若|a|=|b|,则.②若|a|<|b|,则a<b.③若a=b﹣,则(﹣a)2=b2.其中正确的判断的个数是()A.3B.2C.1D.08.图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.∠EFB=65°,则∠AED′等于()A、70°B、65°C、50°D、25°9.如图,下列各式中正确的是()A.B.C.D.10.一正数的平方根是和,则这个正数是…………………………()A.1B.3C.4D.9二、填空题:(每题3分,共30分)11、用吸管吸易拉罐内的饮料时,如图所示,∠1=108°,则∠2=_____________;12、已知直线AB和CD相交与点O,OE平分∠BOC,已知∠BOE=65°,则∠AOC=______;13、已知AD∥BC,BD平分∠ABC,∠A=116°,则∠DBC=____________14.自来水公司为某小区A改造供水系统,如图沿路线AO铺设管道和BO主管道衔接(AOBO⊥),路线最短,工程造价最低,根据是_________.15下列说法中①0.09是0.81的平方根;②-9的平方根是±3;③2(5)的算术平方根是-5;④2是一个负数;⑤0的相反数和倒数都是0;⑥42;⑦已知a是实数,则2||aa;⑧全体实数和数轴上的点一一对应.正确的个数是.EDCBA43211题图11题图12题图13题图16.若实数x、y满足方程330xy,则x与y的关系是17如图,点D在AC上,点E在AB上,且BDCE⊥,垂足为点M.下列说法:①BM的长是点B到CE的距离;②CE的长是点C到AB的距离;③BD的长是点B到AC的距离;④CM的长是点C到BD的距离.其中正确的是_________(填序号).18.如果的平方根是,则=.19若的整数部分为,小数部分为,的值是__________。20若=5.036,=15.906,则=__________。三.计算题:4x2-16=027(x-3)3=-64+-22已知2a-1的平方根是±3,3a+b-1的算术平方根是4,求a+2b的值。(4分)若:则:·等于多少?三、解答题:如图,直线AB、CD相交于点O,OE⊥CD于O,OD平分∠BOF,若∠BOE=55°,试求∠AOC和∠AOF的度数。(5分)如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.填写证明过程的理由.(4分)证明:∵∠1=∠2(已知)∠2=∠3∠1=∠4()∴∠3=∠4()∴_____∥_____()∴∠C=∠ABD()∵∠C=∠D(已知)∴∠D=∠ABD()∴DF∥AC()ABCDEF1423PDCBAFEDCBA填空:已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,请说明CD⊥AB的理由.(4分)答:理由:∵∠1=∠ACB()∴DE∥BC()∴∠2=()∵∠2=∠3(已知)∴∠3=∴CD∥FH()∴∠BDC=∠BHF()又∵FH⊥AB(已知)∴.如图(1)(2)(3)中,都满足AB∥CDABCD(1)(2)(3)试求:(1)图(1)中∠A+∠C的度数,并说明理由。(2)图(2)中∠A+∠APC+∠C的度数,并说明理由。(3)图(3)中∠A+∠AEF+∠EFC+∠C的度数,并简要说明理由。(4)按上述规律,∠A+……+∠C(共有n个角的相加)的和为(7分)CABDEFH123