你能证明它们吗(2)等腰三角形的判定VIP免费

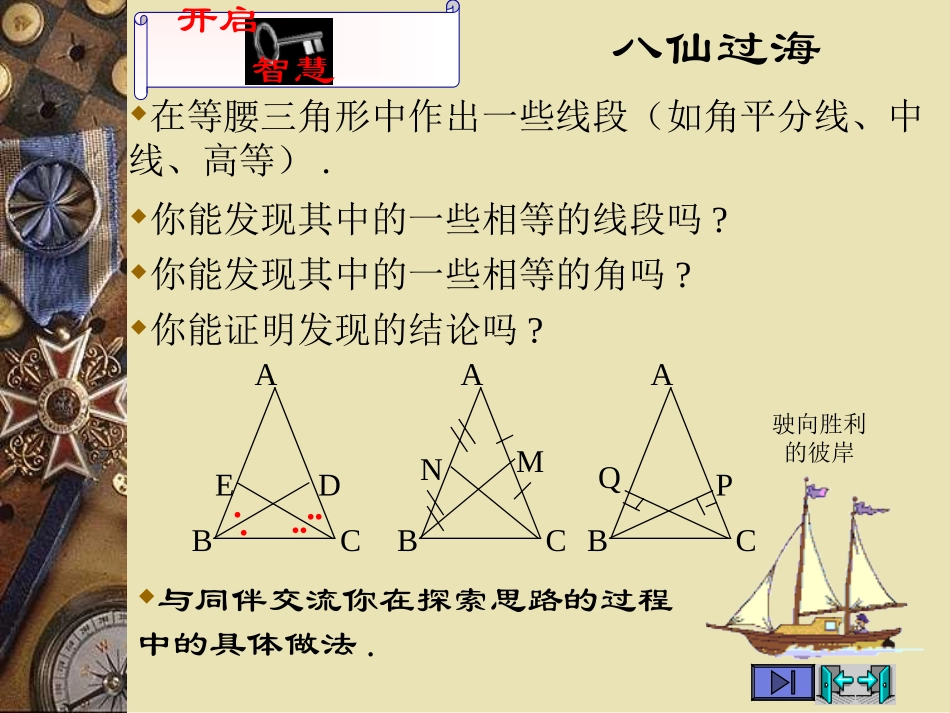
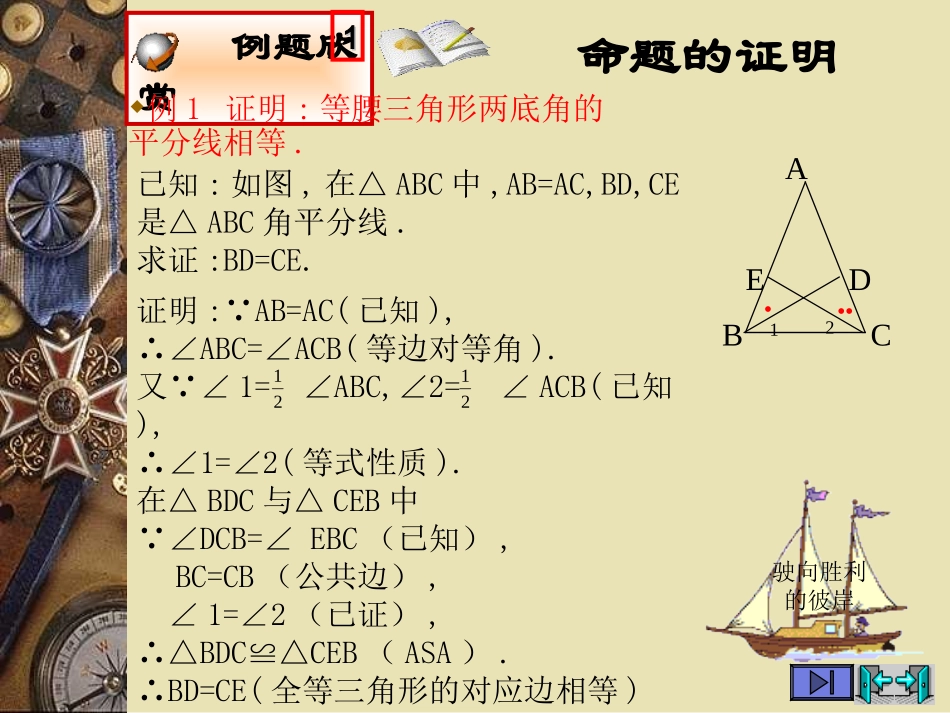
九年级数学（上册）第一章证明(二)和平县实验初级中学驶向胜利的彼岸八仙过海在等腰三角形中作出一些线段（如角平分线、中线、高等）.与同伴交流你在探索思路的过程中的具体做法.你能发现其中的一些相等的线段吗?你能发现其中的一些相等的角吗?ACB你能证明发现的结论吗?D●●E●●●●ACBMNACBPQ开启智慧驶向胜利的彼岸命题的证明例题欣赏11例1证明:等腰三角形两底角的平分线相等.证明: AB=AC(已知),∴∠ABC=∠ACB(等边对等角).又 ∠1=∠ABC,∠2=∠ACB(已知),∴∠1=∠2(等式性质).在△BDC与△CEB中 ∠DCB=∠EBC（已知）,BC=CB（公共边）,∠1=∠2（已证）,∴△BDC≌△CEB（ASA）.∴BD=CE(全等三角形的对应边相等)已知:如图,在△ABC中,AB=AC,BD,CE是△ABC角平分线.求证:BD=CE.ACBD●1E●●22121驶向胜利的彼岸命题的证明我能行111证明:等腰三角形两腰上的中线相等.证明: AB=AC(已知),∴∠ABC=∠ACB(等边对等角).又 CM=AC,BN=AB(已知),∴CM=BN(等式性质).在△BMC与△CNB中 BC=CB（公共边）,∠MCB=∠NBC（已知）,CM=BN（已证）,∴△BMC≌△CNB（SAS）.∴BM=CN(全等三角形的对应边相等)已知:如图,在△ABC中,AB=AC,BM,CN是△ABC两腰上的中线.求证:BM=CN.2121ACBMN驶向胜利的彼岸命题的证明我能行222证明:等腰三角形两腰上的高相等.证明: AB=AC(已知),∴∠ABC=∠ACB(等边对等角). BP,CQ是△ABC两腰上的高(已知),∴∠BPC=∠CQB=900(高的定义).又 BC=CB（公共边）,∴△BPC≌△CQB（AAS）.∴BP=CQ(全等三角形的对应边相等)已知:如图,在△ABC中,AB=AC,BP,CQ是△ABC两腰上的高.求证:BP=CQ.ACBPQ议一议11′驶向胜利的彼岸ACBD●E●1.已知:如图,在△ABC中,(1)如果，,那么BD=CE吗?如果，呢?由此你能得到一个什么结论?(2)如果,,那么BD=CE吗?如果,呢?由此你能得到一个什么结论?(3)你能证明得到的结论吗？13ABDABC14ABDABC14ABDABC1AD=AC31AE=AB31AD=AC41AE=AB414ABDABC13ABDABC等腰三角形的判定议一议22你是如何思考的，请与同伴交流你的做法.′驶向胜利的彼岸2.前面已经证明了“等边对等角”，反过来，“等角对等边”吗?即有两个角相等的三角形是等腰三角形吗?ACB已知:如图,在△ABC中,∠B＝∠C.求证:AB=AC.分析:要证明AB=AC,只要能构造出AB，AC所在的两个三角形全等就可以了.如：作BC边上的中线；作∠A的平分线或作BC边上的高.几何的三种语言议一议33′驶向胜利的彼岸定理：有两个角相等的三角形是等腰三角形（等角对等边）.ACB在△ABC中 ∠B＝∠C（已知），∴AB=AC（等角对等边）.这又是一个判定两条线段相等根据之一.学无止境小明说,在一个三角形中，如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗?如果成立,你能证明它吗?′驶向胜利的彼岸开启智慧CAB●●●即在△ABC中,如果∠B≠C,∠那么AB≠AC.证明命题的新思路路边苦李古时候有个人叫王戍，7岁那年的某一天和小朋友在路边玩，看见一棵李子树上的果实多得把树枝都快压断了，小朋友们都跑去摘，只有王戍站着没动。小朋友问他为何不去摘，他说：“树长在路边，李子那么多，肯定李子是苦的，不好吃。不然早就没了！”。小朋友摘来一尝，李子果然苦的没法吃。′驶向胜利的彼岸开启智慧学无止境小明是这样想的:如图,在△ABC中,已知∠B≠∠C,此时,AB与AC要么相等,要么不相等.你能理解他的推理过程吗?′驶向胜利的彼岸开启智慧CAB●●●假设AB=AC,那么根据“等边对等角”∠B=∠C,但已知条件是∠B≠∠C.“∠B=∠C”与“∠B≠∠C”相矛盾，因此，AB≠AC.反证法小明在证明时，先假设命题的结论不成立，然后推导出与定义，公理、已证定理或已知条件相矛盾的结果，从而证明便是的结论一定成立.这种证明方法称为反证法(reductiontoabsurdity)假设AB=AC,那么根据“等角对等边”∠B=∠C,但已知条件是∠B≠∠C.“∠B=∠C”与“∠B≠∠C”相矛盾,因此,AB≠AC.驶向胜利的彼岸开启智慧反证法是一种重要的数学证明方法.在解决某些问题时常常会有出人意料的作用.CAB●●●反证法1.假设:先假设命题的结论不成立;2.归谬:从这个假设出发,应用正确的推论方法,得出...