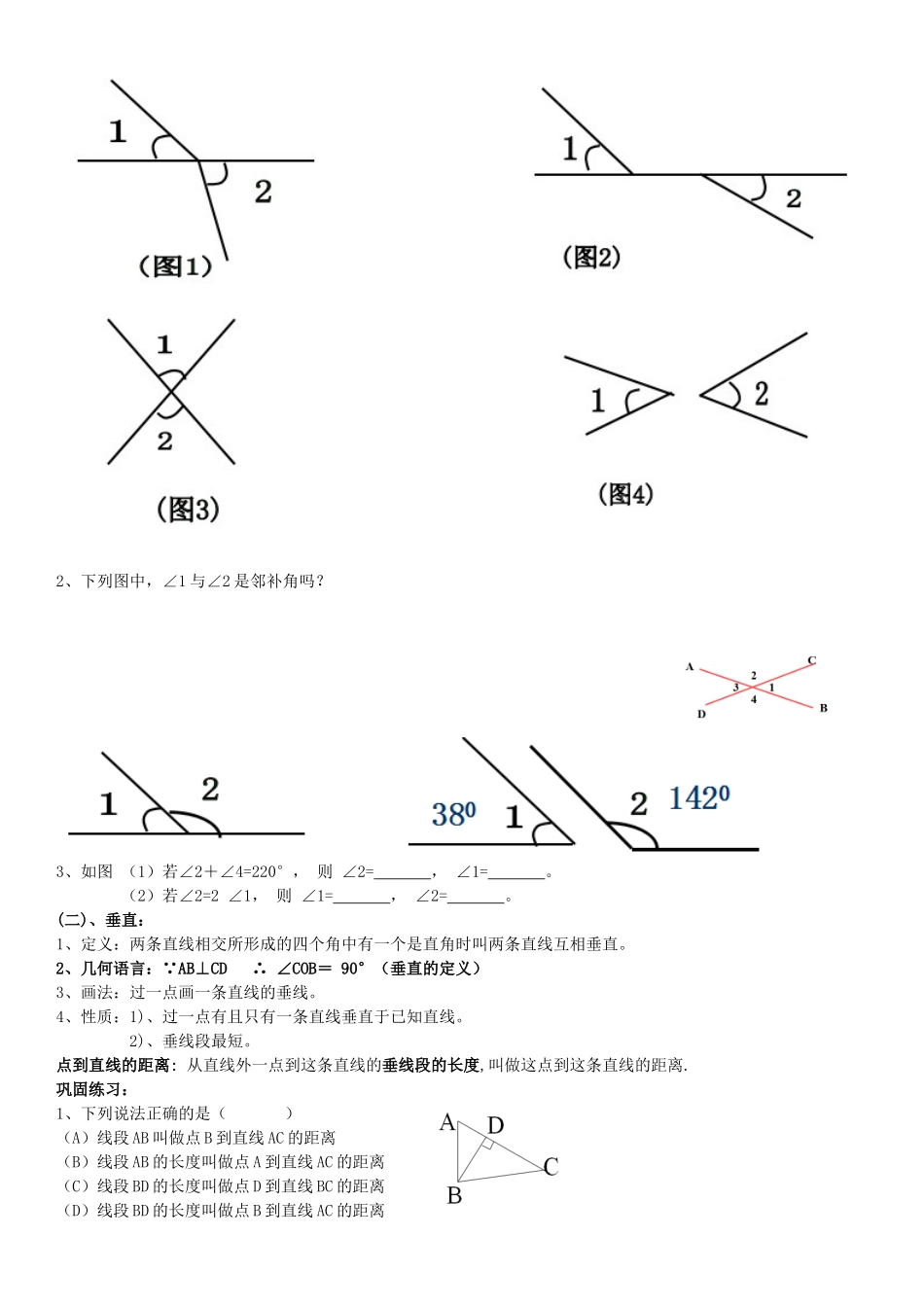
相交线与平行线复习课学案碧华学校陈瑞汕一、学习目标1、进一步巩固邻补角、对顶角的概念和性质2、理解垂线、垂线段的概念和性质3、掌握两条直线平行的判定和性质4、通过平移,理解图形平移变换的性质5、能区分命题的题设和结论以及命题的真假二、重点和难点重点:垂线的性质和平行线的判定和性质。难点:平行线的判定和性质。(一)、相交:1、对顶角:性质:对顶角相等。2、邻补角:性质:同角的补角相等。典型例题1、下列图中,∠1与∠2是对顶角吗?为什么?2、下列图中,∠1与∠2是邻补角吗?3、如图(1)若∠2+∠4=220°,则∠2=,∠1=。(2)若∠2=2∠1,则∠1=,∠2=。(二)、垂直:1、定义:两条直线相交所形成的四个角中有一个是直角时叫两条直线互相垂直。2、几何语言:∵AB⊥CD∴∠COB=90°(垂直的定义)3、画法:过一点画一条直线的垂线。4、性质:1)、过一点有且只有一条直线垂直于已知直线。2)、垂线段最短。点到直线的距离:从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离.巩固练习:1、下列说法正确的是()(A)线段AB叫做点B到直线AC的距离(B)线段AB的长度叫做点A到直线AC的距离(C)线段BD的长度叫做点D到直线BC的距离(D)线段BD的长度叫做点B到直线AC的距离2、如图,已知AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°求∠COE、∠AOE、∠AOG的度数.(三)、三线八角:角的名称位置特征基本图形相同点共同特征同位角在截线的同侧,在被截两直线的同旁。同旁内角在截线的同侧,在被截两直线之间。内错角在截线的两侧,在被截两直线之间。典型例题(1)∠1和∠9是由直线、被直线所截成的角(2)∠6和∠12是由直线、被直线所截成的角(3)∠4和∠6是由直线、被直线所截成的角易错点如图中的∠1和∠2是同位角吗?为什么?(四)、平行:1、定义:同一平面内,不相交的两条直线叫做平行线。2、几何语言:常用“//”表示平行3、画法:过一点画一条直线的平行线。一放二靠三移(推)四画4、平行公理及推论:经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行(平行公理推论)定理:在同一个平面内,垂直于同一条直线的两条直线平行。5、平行线的判定和性质典型例题:1.如图,填空(1)∵∠B=∠1(已知)∴____//____()(2)∵CG//DF(已知)∴∠2=_____()(3)∵∠3=∠A(已知)∴____//____()(4)∵AG//DF(已知)∴∠3=_____()(5)∵∠B+∠4=180°(已知)∴____//____()(6)∵CG//DF(已知)∴∠F+_____=180°()2、已知:如图,CD⊥DA,DA⊥AB,∠1=∠2,试确定射线DF与AE的位置关系,并说明你的理由.(1)问题的结论:DF______AE.(2)证明思路分析:欲证DF______AE,只要证∠3=______.(3)证明过程:证明:∵CD⊥DA,DA⊥AB,()∴∠CDA=∠DAB=______°.(垂直定义)又∠1=∠2,()从而∠CDA-∠1=______-______,(等式的性质)即∠3=______.∴DF______AE.(___________,___________)3.已知∠DAC=∠ACB,∠D+∠DFE=180°,求证:EF//BC4.已知EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。平行条件结论平行线的判定平行线的性质综合提高:已知:如图AB∥CD,试探究∠AEC与∠A,∠C的关系练习:⒈如图⑴,已知AB∥CD,∠1=30°,∠2=90°,则∠3=______°⒉如图⑵,若AE∥CD,∠EBF=135°,∠BFD=60°,∠D=()A、75°B、45°C、30°D、15°思考题3、如图,已知AB∥CD,∠ABF=∠DCE.试说明:∠BFE=∠FEC.4、如图,已知∠AEM=∠DGN,则你能说明AB平行于CD吗?变式:若∠AEM=∠DGN,EF、GH分别平分∠AEG和∠CGN,则图中还有平行线吗?课堂小结:本节课重点掌握垂线的性质和平行线的判定方法和性质。