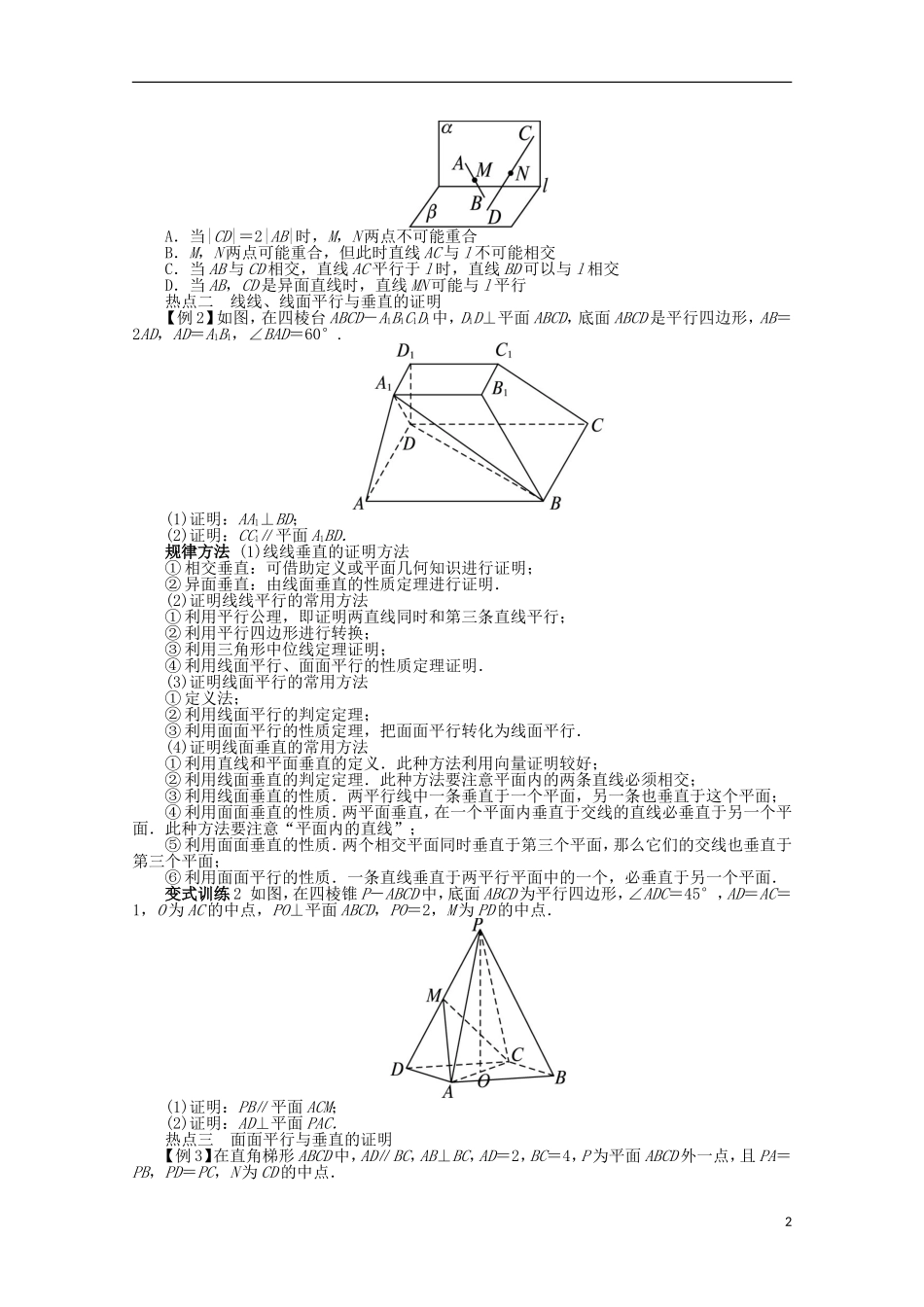
专题五立体几何第2讲点、直线、平面之间的位置关系真题试做1.(2012·四川高考,文6)下列命题正确的是().A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行2.(2012·浙江高考,文5)设l是直线,α,β是两个不同的平面,().A.若l∥α,l∥β,则α∥βB.若l∥α,l⊥β,则α⊥βC.若α⊥β,l⊥α,则l⊥βD.若α⊥β,l∥α,则l⊥β3.(2012·大纲全国高考,文16)已知正方体ABCD-A1B1C1D1中,E,F分别为BB1,CC1的中点,那么异面直线AE与D1F所成角的余弦值为__________.4.(2012·辽宁高考,文16)已知点P,A,B,C,D是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为2的正方形.若PA=2,则△OAB的面积为__________.5.(2012·浙江高考,文20)如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.(1)证明:①EF∥A1D1;②BA1⊥平面B1C1EF;(2)求BC1与平面B1C1EF所成的角的正弦值.考向分析从近几年的高考试题来看,在本讲中所涉及的主要内容是:(1)有关线面位置关系的组合判断,试题以选择题的形式出现,通常是考查空间线线、线面、面面位置关系的判定与性质;(2)有关线线、线面平行与垂直的证明,试题以解答题为主,常以多面体为载体,突出考查学生的空间想象能力及推理论证能力;(3)有关面面平行与垂直的证明,多以解答题的形式出现,综合性强;(4)有关折叠问题,以解答题为主,通过折叠把平面图形转化为空间几何体,更好地考查学生的空间想象能力和知识迁移能力.预测2013年高考中,仍以某几何体为载体,重在探索和判定线线、线面和面面的位置关系,当然也可能综合考查面积及体积的计算,题目难度为中低档.热点例析【例1】热点一有关线面位置关系的组合判断若a,b是两条异面直线,α,β是两个不同平面,a⊂α,b⊂β,α∩β=l,则().A.l与a,b分别相交B.l与a,b都不相交C.l至多与a,b中一条相交D.l至少与a,b中的一条相交规律方法解决空间线面位置关系的组合判断题常有以下方法:(1)根据空间线面垂直、平行关系的判定定理和性质定理逐项判断来解决问题;(2)必要时可以借助空间几何模型,如从长方体、四面体等模型中观察线面位置关系,并结合有关定理来进行判断;(3)应熟练掌握立体几何的三种语言——符号语言、自然语言以及图形语言的相互转换.变式训练1如图所示,平面α⊥平面β,α∩β=直线l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∉直线l,M,N分别是线段AB,CD的中点.下列判断正确的是().1A.当|CD|=2|AB|时,M,N两点不可能重合B.M,N两点可能重合,但此时直线AC与l不可能相交C.当AB与CD相交,直线AC平行于l时,直线BD可以与l相交D.当AB,CD是异面直线时,直线MN可能与l平行热点二线线、线面平行与垂直的证明【例2】如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.(1)证明:AA1⊥BD;(2)证明:CC1∥平面A1BD.规律方法(1)线线垂直的证明方法①相交垂直:可借助定义或平面几何知识进行证明;②异面垂直:由线面垂直的性质定理进行证明.(2)证明线线平行的常用方法①利用平行公理,即证明两直线同时和第三条直线平行;②利用平行四边形进行转换;③利用三角形中位线定理证明;④利用线面平行、面面平行的性质定理证明.(3)证明线面平行的常用方法①定义法;②利用线面平行的判定定理;③利用面面平行的性质定理,把面面平行转化为线面平行.(4)证明线面垂直的常用方法①利用直线和平面垂直的定义.此种方法利用向量证明较好;②利用线面垂直的判定定理.此种方法要注意平面内的两条直线必须相交;③利用线面垂直的性质.两平行线中一条垂直于一个平面,另一条也垂直于这个平面;④利用面面垂直的性质.两平面垂直,在一个平面内垂直于交线的直线必垂直于另一个平面.此...