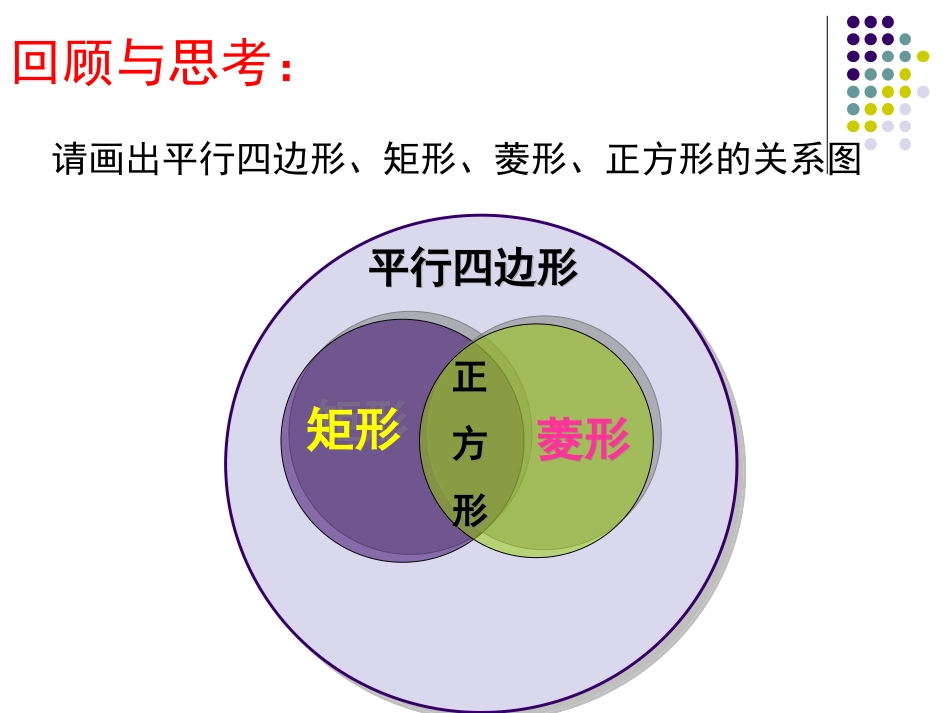
贺兰四中张君店平行四边形平行四边形矩形矩形菱形菱形正方形正方形请画出平行四边形、矩形、菱形、正方形的关系图回顾与思考:正方形的性质=正方形的两条对角线互相垂直平分且相等,每条对角线平分一组对角正方形的四条边相等正方形的四个角都是直角正方形的性质边角对角线一个角是直角有一个角是直角且一组邻边相等的平行四边形叫做正方形正方形平行四边形正方形的定义一组邻边相等定义能否作为依据来判定四边形是正方形呢?正方形矩形有一组邻边相等菱形有一个角是直角有一组邻边相等有一个角是直角平行四边形有一个角是直角有一组邻边相等解读定义:矩形矩形菱形菱形正方形正方形有一组邻边相等有一个角是直角识别正方形的方法识别正方形的方法从而我们得出:♥一组邻边相等的矩形是正方形。♥有一个内角是直角的菱形是正方形。既是矩形又是菱形的四边形是正方形。平行四边形、矩形、菱形的判定5种识别方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直7777老师说下列三个图形都是正方形,你相信吗?555555552525有一组邻边相等并且有一个角是直角的平行四边形是正方形。一个内角为直角的菱形是正方形。两条对角线互相垂直平分且相等的四边形是正方形。合作探究合作探究有一组邻边相等并且有一个角是直角的平行四边形是正方形。既是矩形又是菱形(或者既是菱形又是矩形)的四边形是正方形。1、定义法:2、矩形菱形法:3、对角线法:两条对角线互相垂直平分且相等的四边形是正方形。1)一组邻边相等的矩形是正方形2)有一个角是直角的菱形是正方形想一想:还可以怎样表达呢?1)对角线互相垂直的矩形是正方形2)对角线相等的菱形是正方形。归纳总结:①、对角线相等的菱形是正方形②、对角线互相垂直的矩形是正方形③、对角线互相垂直且相等的四边形是正方形④四条边都相等的四边形是正方形⑤、四个角都相等的四边形是正方形⑥、四边相等,有一个角是直角的四边形是正方形.()()()()()()1、判断对错当堂检测:2、下列命题正确的是()A、四个角都相等的四边形是正方形B、四条边都相等的四边形是正方形C、对角线相等的平行四边形是正方形D、对角线互相垂直的矩形是正方形2、下列命题正确的是()A、四个角都相等的四边形是正方形B、四条边都相等的四边形是正方形C、对角线相等的平行四边形是正方形D、对角线互相垂直的矩形是正方形DD3、四个内角都相等,四条边也都相等的四边形一定是:()A.正方形B.菱形C.矩形D.平行四边形A已知:平行四边形ABCD的对角线AC、BD交于点O,从下列条件中取出哪两个条件后,可使平行四边形ABCD成为正方形?(1)AB=AD;(2)AC=BD;(3)∠BAD=90;(4)AC⊥BD。ABCDO合作探究合作探究矩形菱形(2)(3)(1)(4)平行四边形正方形(1)AB=AD;(2)AC=BD;(3)∠BAD=90;(4)AC⊥BD。ABCDODOABC解题小结:正方形即是特殊的矩形,又是特殊的菱形。它没有明确的判定定理,要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形,从而得到这个四边形是正方形。如图1-21,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BFCE∥,CFBE∥.求证:四边形BECF是正方形.证明: BFCE∥,CFBE∥,∴四边形BECF是平行四边形. 四边形ABCD是矩形,∴∠ABC=90°,∠DCB=90°.又 BE平分∠ABC,CE平分∠DCB,∴∠EBC=45°,∠ECB=45°.∴∠EBC=ECB∠.∴EB=EC.□∴BECF是菱形(菱形的定义).在△EBC中, ∠EBC=45°,∠ECB=45°,∴∠BEC=90°.∴菱形BECF是正方形(有一个角是直角的菱形是正方形).ABCDEF1.从长方形木板中怎样截出最大的正方形木板?2.怎样使菱形的衣帽架变成正方形的衣帽架?学以致用:课堂小结:本节课你学到了哪些判定正方形的方法呢?你还存在哪些困惑呢?有一组邻边相等并且有一个角是直角的平行四边形是正方形。既是矩形又是菱形(或者既是菱形又是矩形)的四边形是正方形。1、定义法:2、矩形菱形法:3、对角线法:两条对角线互相垂直平分且相等的四边形是正方形。1)一组邻边相等的矩形是正方形2)有一个角是直角的菱...