导数的几何意义VIP免费

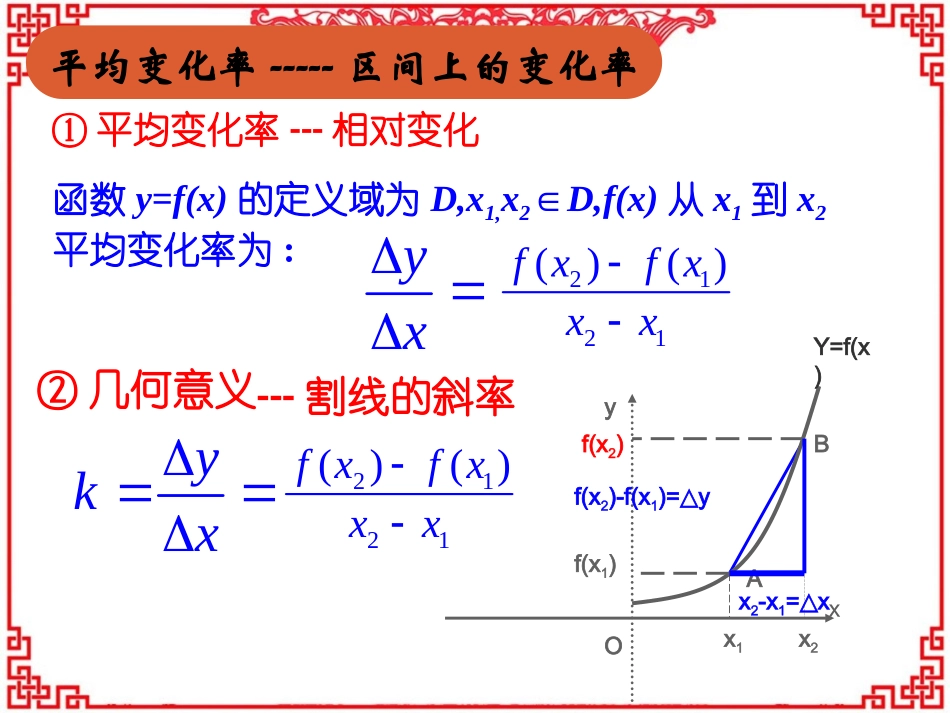
导数的几何意义①平均变化率---相对变化函数y=f(x)的定义域为D,x1,x2D,f(x)∈从x1到x2平均变化率为:yx2121()()fxfxxx②几何意义OABxyY=f(x)x1x2f(x1)f(x2)x2-x1=x△f(x2)-f(x1)=y△ykx2121()()fxfxxx平均变化率-----区间上的变化率---割线的斜率函数y=f(x)在x0附近的平均变化率为:yx00()()fxxfxx平均变化率-----点附近的变化率00000()()()limlimxxfxxfxyfxxx导数-----瞬时变化率平均变化率的极限)(xfy0x求函数在处的导数的步骤（1）求绝对变化量：（3）取极限：（2）求平均变化率：前提是要清楚初末状态00()()yfxxfx00()()fxxfxyxx00()limxyfxx求一点处导数的步骤探究导数的几何意义PQoxyy=f(x)割线切线T我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.00000()()()limlimxxfxxfxykfxxx切线函数在x=x0处的导数就是函数在该点的切线斜率。要注意切线与整个图象可能有多个交点。Poxy割线切线T01/15/2025例1、如图，它表示跳水运动中高度随时间变化的函数h(t)=-4.9t2+6.5t+10的图象。根据图象，请描述、比较曲线h(t)在t0,t1,t2附近的变化情况。htol2l0t4t3t2t0t1l1htol2l0t4t3t2t0t1l1例题分析求切线方程的一般步骤：001(,);Pxy（）切点02();kfx（）斜率003()yykxx（）点斜式例2:求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.00()()()limlimxxyfxxfxfxyxx在不致发生混淆时，导函数也简称导数．000()()()()().yfxxfxfxfxx函数在点处的导数等于函数的导函数在点处的函数值由函数f(x)在x=x0处求导数的过程可以看到,当时,f’(x0)是一个确定的数.那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.即:导函数的定义如何求函数y=f(x)的导数?(1)()();yfxxfx求函数的增量(2):()();yfxxfxxx求函数的增量与自变量的增量的比值0(3)()lim.xyyfxx求极限，得导函数例3:求f(x)=x2+1的导函数.