三角函数平移变换和周期变换VIP免费

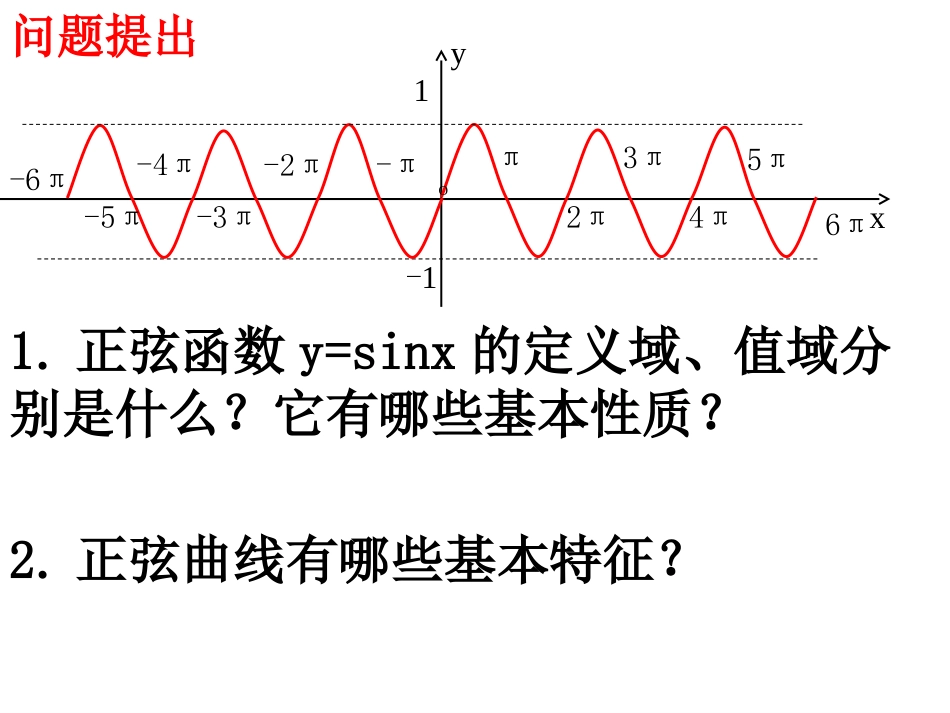
图像变换高一(13)班汤勇问题提出1.正弦函数y=sinx的定义域、值域分别是什么？它有哪些基本性质？2.正弦曲线有哪些基本特征？y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-π4.下面就来探索、、A对函数的图象的影响.3.正弦函数y=sinx是最基本、最简单的三角函数，在物理中，简谐运动中的单摆对平衡位置的位移y与时间x的关系，交流电的电流y与时间x的关系等都是形如的函数.那么函数与函数y=sinx有什么关系呢?从解析式上来看函数y=sinx就是函数在A=1，ω=1，的情况.)sin(xAy)sin(xAy)sin(xAy0)sin(xAy探究一：对的图象的影响)sin(xy思考1：函数周期是T=____;你有什么办法画出该函数在一个周期内的图象？)3sin(xyπ2πoyx267633235)3sin(xy时的情形取先考虑3xsinx22302010-103x363267352π思考2：比较函数与的图象的形状和位置，你有什么发现？xysin)3sin(xy函数的图象，可以看作是把正弦函数的图象上所有的点向左平移个单位长度而得到的.)3sin(xyxysin3)3sin(xysinyx=的图象xysin的图象)3sin(xy3向左平移6π2πoyx2332356703＞思考3：用“五点法”作出函数在一个周期内的图象，比较它与函数的图象的形状和位置，你又有什么发现？)3sin(xyxysin)3sin(xy3373461165π2πoyx2sinyx=的图象xysin的图象)3sin(xy3向右平移03＜思考4：一般地，对任意的（≠0），函数的图象是由函数的图象经过怎样的变换而得到的？)sin(xyxysin的图象，可以看作是把正弦函数的图象上所有的点向左（当＞0时）或向右（当＜0时）平行移动||个单位长度而得到.)sin(xyxysin的图象xysin的图象)sin(xy向右平移0＜向左平移0＞思考5：上述变换称为平移变换，据此理论，函数的图象可以看作是把函数y=sinx的图象向________平移_____个单位长度而得到.)6sin(xy6左还是右右探究二：（＞0）对的图象的影响)sin(xy思考1：函数周期T=_____;如何用“五点法”画出该函数在一个周期内的图象？)32sin(xyπ2πoyx2)32sin(xy312712656看下面的问题的情形为此先考虑象之间的关系的图观察它们与值，作出它们的图象，取任意不同的，可对为了研究方便，不妨令.2.)3sin(3xyxsinx22302010-1032x612312765思考2：比较函数与的图象的形状和位置，你有什么发现？)32sin(xy)3sin(xy353312712656π2πoyx2)32sin(xy)3sin(xy的图象)3sin(xy的图象)32sin(xy纵坐标不变所有的点横坐标缩短到原来的倍21思考3：用“五点法”作出函数在一个周期内的图象，比较它与函数的图象的形状和位置，你又有什么发现？)3sin(xy)321sin(xy353π2πoyx23π2p-3237343103)321sin(xy)3sin(xy的图象xysin的图象)32sin(xy所有的点横坐标伸长到原来的2倍纵坐标不变思考4：一般地，对任意的（＞0），函数的图象是由函数的图象经过怎样的变换而得到的？)sin(xy)sin(xy函数的图象，可以看作是把函数的图象上所有点的横坐标缩短（当＞1时）或伸长（当0＜＜1时）到原来的倍（纵坐标不变）而得到的.)sin(xy)sin(xy1的图象)sin(xy的图象)sin(xy纵坐标不变所有的点横坐标伸长到原来的倍1上所有的点横坐标伸长到原来的1.5倍（纵坐标不变）而得到的.思考5：上述变换称为周期变换据此理论，函数的图象可以看作是把函数的图象)6sin(xy)632sin(xy进行怎样变换而得到的？思考6：函数的图象，可以看作是把函数的图象进行怎样变换而得到的？xysin)632sin(xy6p函数的图象，可以看作是先把的图象向右平移,再把所得的图象上所有的点的横坐标伸长到原来的倍（纵坐标不变）而得到的.)632sin(xysinyx=623的图象)6sin(xy的图象)63...