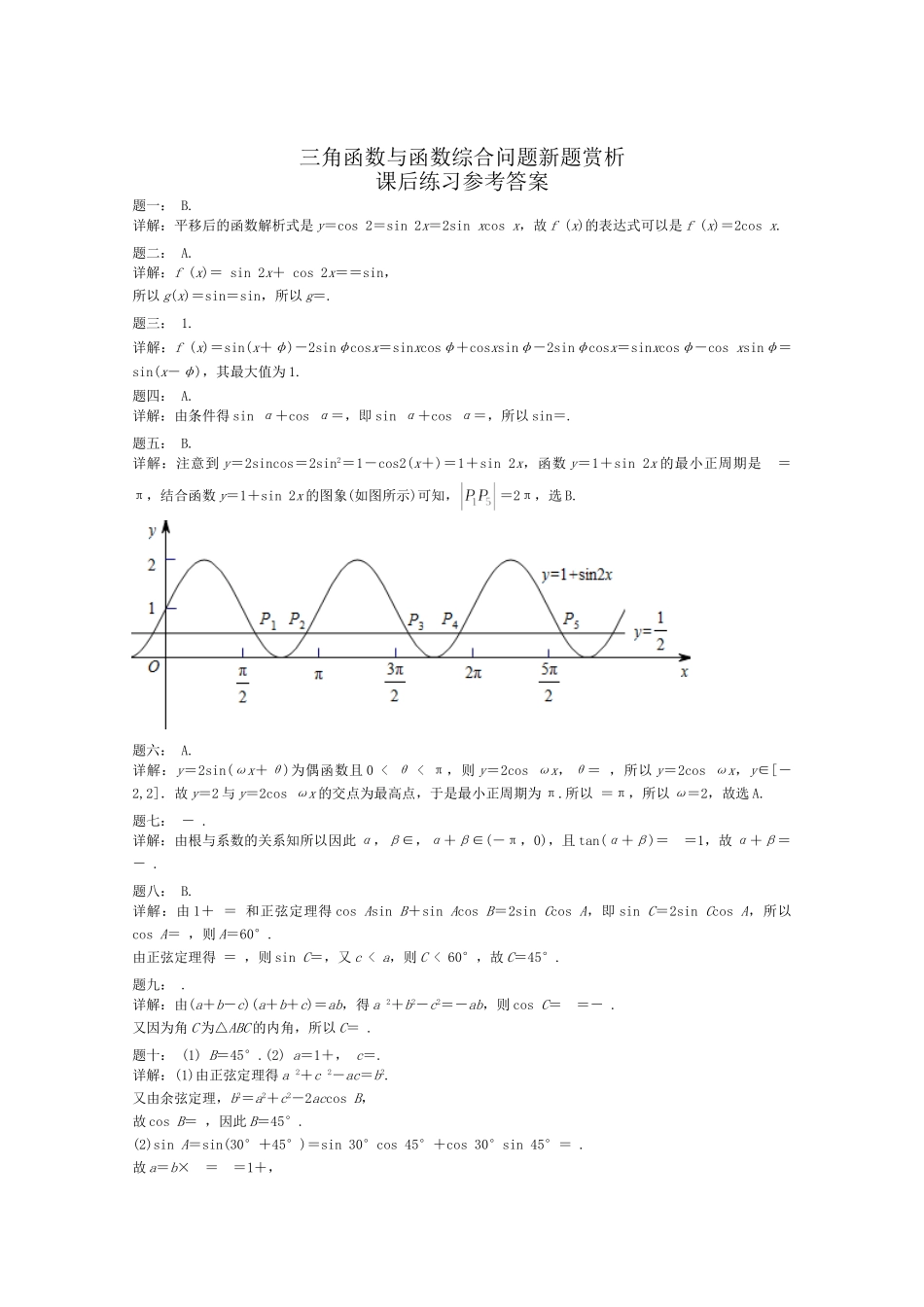
三角函数与函数综合问题新题赏析课后练习题一:将函数y=cos2x的图象向右平移个单位,得到函数y=f(x)·sinx的图象,则f(x)的表达式可以是().A.f(x)=-2cosxB.f(x)=2cosxC.f(x)=sin2xD.f(x)=(sin2x+cos2x)题二:将函数f(x)=sin2x+cos2x的图象向右平移个单位后得到函数g(x)的图象,则g的值为().A.B.-1C.D.2题三:函数f(x)=sin(x+φ)-2sinφcosx的最大值为________.题四:已知sin+cosα=,则sin的值为().A.B.C.D.题五:已知曲线y=2sin·cos与直线y=相交,若在y轴右侧的交点自左向右依次记为P1,P2,P3…,,则等于().A.πB.2πC.3πD.4π题六:已知函数y=2sin(ωx+θ)为偶函数(0<θ<π),其图象与直线y=2的交点的横坐标为x1,x2,若|x1-x2|的最小值为π,则().A.ω=2,θ=B.ω=,θ=C.ω=,θ=D.ω=2,θ=题七:已知α,β∈,且tanα,tanβ是方程x2+6x+7=0的两个根,则α+β=________.题八:在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2,c=2,1+=,则C=().A.30°B.45°C.45°或135°D.60°题九:设△ABC的内角A,B,C所对的边分别为a,b,c.若(a+b-c)(a+b+c)=ab,则角C=________.题十:△ABC的内角A,B,C的对边分别为a,b,c,且asinA+csinC-asinC=bsinB.(1)求B;(2)若A=75°,b=2,求a,c.题十一:已知函数f(x)=sin2x+sinxcosx,x∈(1)求f(x)的零点;(2)求f(x)的最大值和最小值.题十二:已知函数f(x)=sin+cos,x∈R.(1)求f(x)的最小正周期和最小值;(2)已知cos(β-α)=,cos(β+α)=-,0<α<β≤,求证:[f(β)]2-2=0.题十三:已知向量a=(3sinα,cosα),b=(2sinα,5sinα-4cosα),α∈,且a⊥b.(1)求tanα的值;(2)求cos的值.题十四:已知向量a=(m,cos2x),b=(sin2x,n),函数f(x)=a·b,且y=f(x)的图象过点和点.(1)求m,n的值;(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.三角函数与函数综合问题新题赏析课后练习参考答案题一:B.详解:平移后的函数解析式是y=cos2=sin2x=2sinxcosx,故f(x)的表达式可以是f(x)=2cosx.题二:A.详解:f(x)=sin2x+cos2x==sin,所以g(x)=sin=sin,所以g=.题三:1.详解:f(x)=sin(x+φ)-2sinφcosx=sinxcosφ+cosxsinφ-2sinφcosx=sinxcosφ-cosxsinφ=sin(x-φ),其最大值为1.题四:A.详解:由条件得sinα+cosα=,即sinα+cosα=,所以sin=.题五:B.详解:注意到y=2sincos=2sin2=1-cos2(x+)=1+sin2x,函数y=1+sin2x的最小正周期是=π,结合函数y=1+sin2x的图象(如图所示)可知,=2π,选B.题六:A.详解:y=2sin(ωx+θ)为偶函数且0<θ<π,则y=2cosωx,θ=,所以y=2cosωx,y∈[-2,2].故y=2与y=2cosωx的交点为最高点,于是最小正周期为π.所以=π,所以ω=2,故选A.题七:-.详解:由根与系数的关系知所以因此α,β∈,α+β∈(-π,0),且tan(α+β)==1,故α+β=-.题八:B.详解:由1+=和正弦定理得cosAsinB+sinAcosB=2sinCcosA,即sinC=2sinCcosA,所以cosA=,则A=60°.由正弦定理得=,则sinC=,又c