直角三角形的三边关系VIP免费

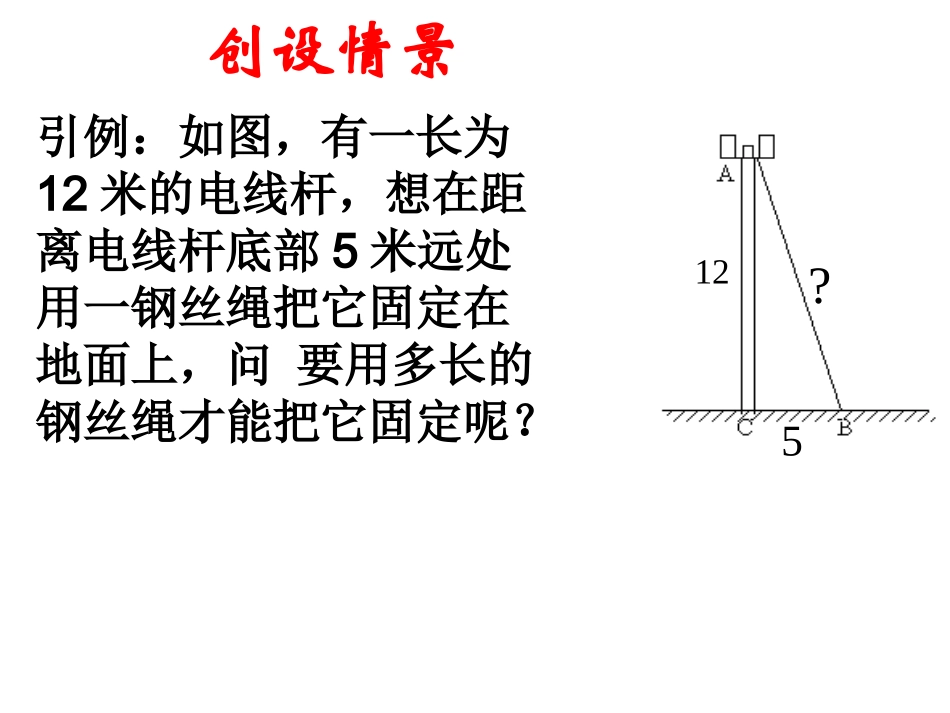
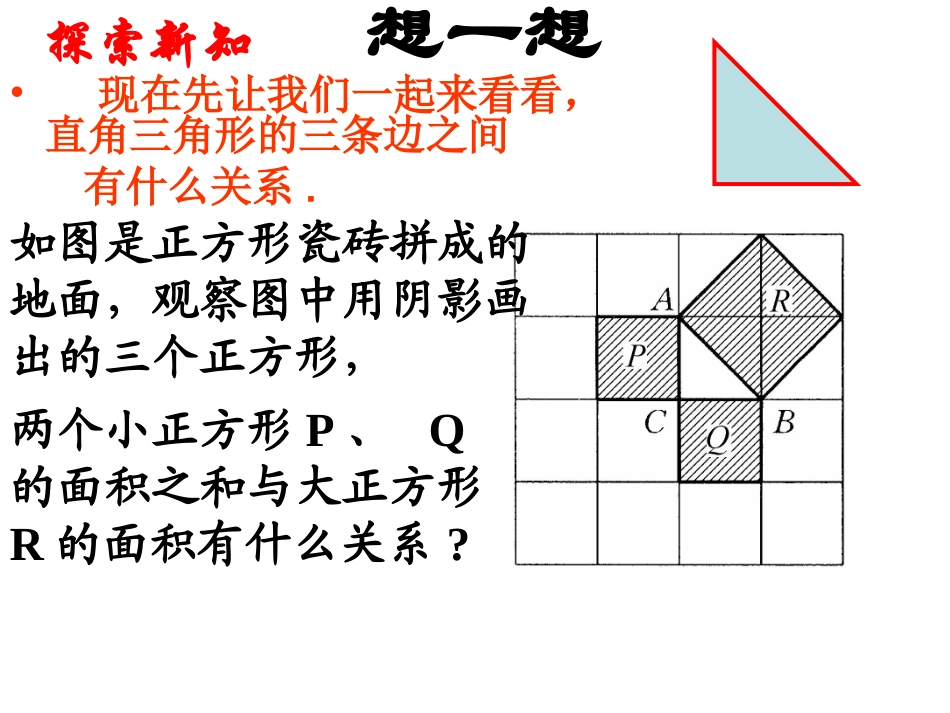
直角三角形三边的关系引例：如图，有一长为12米的电线杆，想在距离电线杆底部5米远处用一钢丝绳把它固定在地面上，问要用多长的钢丝绳才能把它固定呢？125?创设情景想一想•现在先让我们一起来看看，直角三角形的三条边之间有什么关系.探索新知如图是正方形瓷砖拼成的地面，观察图中用阴影画出的三个正方形，两个小正方形P、Q的面积之和与大正方形R的面积有什么关系?RQpSSS（1）三个正方形的面积关系：（2）等腰直角三角形的三边关系：AC2BC2AB2+=说明:在等腰直角三角形ＡＢＣ中，两直角边的平方和等于斜边的平方．问题:在一般的直角三角形中，两直角边的平方和是否等于斜边的平方呢?CBABC2AC2AB2+=222cbaabc9Sp16SQ25SRRQpSSS每一小方格表示1平方厘米PQR试一试•观察图，如果每一小方格表示1平方厘米，•那么可以得到：•正方形P的面积＝_________平方厘米；•正方形Q的面积＝________平方厘米.•正方形R的面积＝________平方厘米.（每一格表示1平方厘米）用等式的形式来表示上面的结论916259+16=25RQpSSS概括•数学上可以说明：对于任意的直角三角形，如果它的两条直角边分别为a、b，斜边为c，那么一定有•a2+b2=c2•这种关系我们称为勾股定理•勾股定理直角三角形两直角边的平方和等于斜边的平方.∟abc做一做在图的方格图中，用三角尺画出两条直角边分别为5cm、12cm的直角三角形，然后用刻度尺量出斜边的长，并验证上述关系对这个直角三角形是否成立.（每一小格代表1平方厘米）勾股定理12?51322213125222cba，bca22222bca22bca22cba，acb222，bac222abc∟勾股定理练习1、求出下列直角三角形中未知边的长度22243x2243x2286y10y∟∟①②3468xy5x勾股定理练习2、求出下列直角三角形中未知边的长度222135x22513x2212y∟∟①②51312xy12222513x251693144勾股定理例题：如图，有一长为12米的电线杆，想在距离电线杆底部5米远处用一钢丝绳把它固定在地面上，问要用多长的钢丝绳才能把它固定呢？解：如图,在Rt△ABC中,∠ACB=90゜AC=12，BC=5,根据勾股定理得：22ACBCAB1312522512勾股定理答：要用13米长的钢丝绳才能把电线杆固定.如图，将长为5.41米的梯子AC斜靠在墙上，ＢＣ长为2.16米，求梯子上端A到墙的底边的垂直距离ＡＢ．（精确到0.01米）5.412.16？试一试勾股定理试一试1、在直角△ABC中，∠C=90°a=3，b=4，则c的值是______.2、在直角△ABC中，∠B=90°,a=3，b=4，则c的值是.3、在△ABC中，a=3，b=4,c=5.则△ABC是三角形.勾股定理1、在RtABC△中，AB＝c,BC=a，AC＝b,B=90∠゜.•(1)已知a=6,b=10,求c；•(2)已知a=24,c=25,求b.勾股定理练习(P51)2、如果一个直角三角形的两条边长分别是3厘米和4厘米，那么这个三角形的周长是多少厘米？可要当心噢！勾股定理练习(P51)勾股定理(P51)复习题A组1.求下列阴影部分的面积：（1）阴影部分是正方形；（2）阴影部分是长方形；（3）阴影部分是半圆．ABCABCABC能力拓展题•欲把一根70cm的木棍放在长、宽、高分别为40cm、30cm、50cm的木箱中，能否放进去！•请说明理由403050是不是所有的三角形的三边都符合勾股定理？如果不是，那么勾股定理是针对哪一类三角形而言的?思考勾股定理揭示了直角三角形三边之间的关系.勾股定理如图所示，一棵大树在一次强烈的地震中于离地面10米处折断倒下，树顶落在离树根24米处.大树在折断之前高多少？2410解：如图，在RtABC△中，∠B=90°，AB=10米，BC=24米，利用勾股定理可以求出折断倒下部分的长度为AC＋AB=26＋10＝36（米）.26241022AC所以，大树在折断之前高为36米.实际应用勾股定理（1）本节课你学到了什么新知识?（2）勾股定理只能用在什么形中？它可以用来解决什么问题？（3）请说出勾股定理得表达式？课堂小结勾股定理