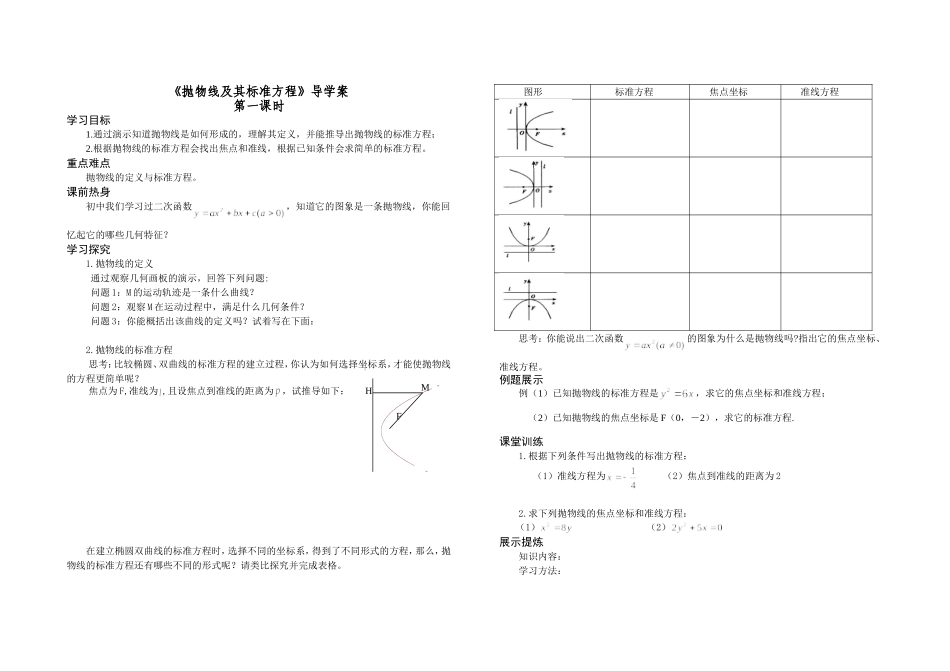
《抛物线及其标准方程》导学案第一课时学习目标1.通过演示知道抛物线是如何形成的,理解其定义,并能推导出抛物线的标准方程;2.根据抛物线的标准方程会找出焦点和准线,根据已知条件会求简单的标准方程。重点难点抛物线的定义与标准方程。课前热身初中我们学习过二次函数,知道它的图象是一条抛物线,你能回忆起它的哪些几何特征?学习探究1.抛物线的定义通过观察几何画板的演示,回答下列问题:问题1:M的运动轨迹是一条什么曲线?问题2:观察M在运动过程中,满足什么几何条件?问题3:你能概括出该曲线的定义吗?试着写在下面:2.抛物线的标准方程思考:比较椭圆、双曲线的标准方程的建立过程,你认为如何选择坐标系,才能使抛物线的方程更简单呢?焦点为F,准线为,且设焦点到准线的距离为,试推导如下:在建立椭圆双曲线的标准方程时,选择不同的坐标系,得到了不同形式的方程,那么,抛物线的标准方程还有哪些不同的形式呢?请类比探究并完成表格。图形标准方程焦点坐标准线方程思考:你能说出二次函数的图象为什么是抛物线吗?指出它的焦点坐标、准线方程。例题展示例(1)已知抛物线的标准方程是,求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.课堂训练1.根据下列条件写出抛物线的标准方程:(1)准线方程为(2)焦点到准线的距离为22.求下列抛物线的焦点坐标和准线方程:(1)(2)展示提炼知识内容:学习方法:FMH数学思想:达标检测:1.准线方程为的抛物线的标准方程为()2.抛物线的焦点坐标为,则抛物线的标准方程为()3.抛物线的焦点坐标为,准线方程为。4.抛物线上一点M到焦点的距离为,则点M到准线的距离是,点M的横坐标是分层作业:基础作业:课本:习题2.2第1、2题拓展作业:1.抛物线的焦点坐标是______________.2.与椭圆有相同的焦点,且顶点在原点的抛物线方程是_____________