反比例函数复习之面积问题VIP免费

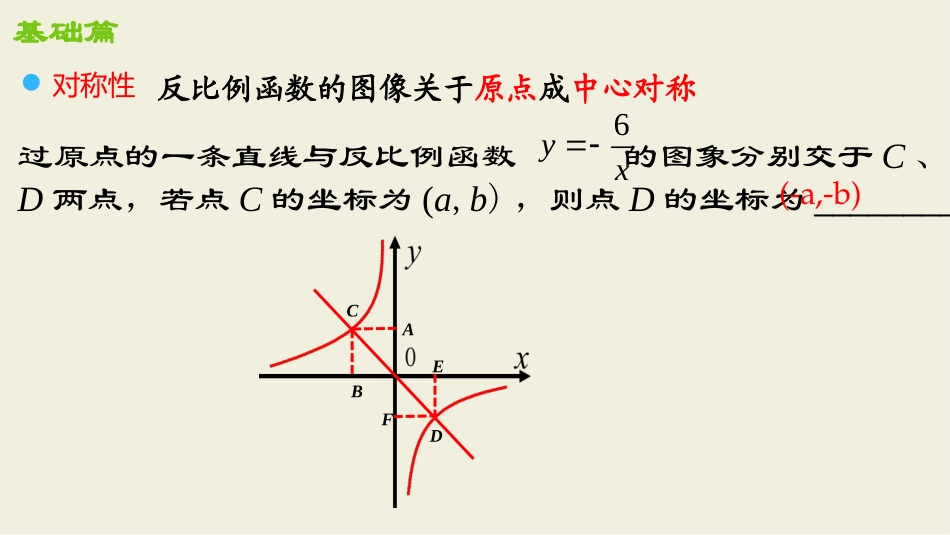
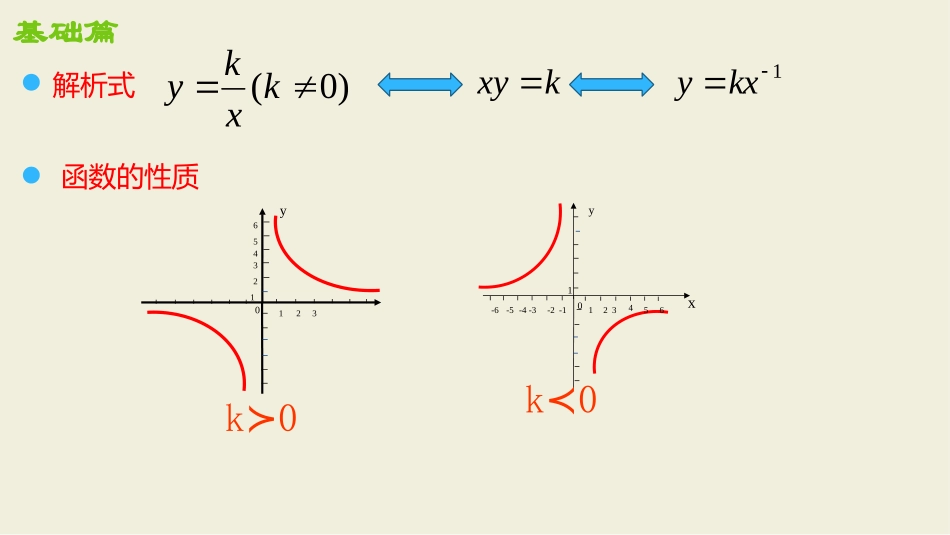反比例函数复习之面积问题基础篇解析式kxy1kxyy0123123456-40-51-3yx2345-16-2-61k0≻k0≺函数的性质)0(kxky基础篇对称性反比例函数的图像关于原点成中心对称过原点的一条直线与反比例函数的图象分别交于C、D两点，若点C的坐标为(a,b)，则点D的坐标为________6yxCDABEF(-a,-b)k的几何意义基础篇kSABOC矩形2kSAOB反比例函数的图像上有一点E，过点E作EP⊥y轴于点P，则△EOP的面积为________.6yx小试牛刀变式：反比例函数的图像上有一点E，过点E作EP⊥y轴于点P，若在x轴上任意取一点F,则△EPF的面积为_________.6yx再显身手已知点A、B分别在反比例函数、的图像上,AB∥x轴，则△ABO的面积是多少？4yx6yxyOBxAC6yx4yx变式：已知点A、B分别在反比例函数、的图像上,AB∥x轴,点F在x轴上任意移动，则△ABF的面积是多少？4yx6yxOBxACFyx6yx4yx变式：平行四边形ABCD的顶点A在反比例函数的图像上，AB∥x轴交y轴于点B,CD在x轴上任意移动，则四边形ABDC的面积是？6yxC’6yx例1：正比例函数的图像与反比例函数的图像交于A、B两点，过点A作AM⊥x轴，垂足为M,连接BM,求SABM△ymx2yx2yx（a，）2a（-a，-）2aCN1.如图，已知反比例函数、，点P（1，1）在上，PC⊥x轴，垂足为C，交于点A,PD⊥y轴，垂足为D，交于点B，求S△PAB11yx22yx1y2y2y、11yx22yx（1，1）练习变式：若点P为在第一象限图像上任一点，求S△PAB1y11yx22yx（a，）a12.已知反比例函数，点A（1，2）在图像上，过点A作AB⊥x轴2yx(1)求S△ABO(2)点C（0，-2）在y轴上，求S△ACO(3)连接A、C和x轴交于点D,求S△AOD练习CD2yx（1，2）-2(4).若点C（2，1）在函数图像上，连接A、C和x轴交于点D，求S△AODCD（1，2）（2，1）3.如图，过点E(1,4)的直线分别交x轴、y轴于点D、C，若直线与双曲线的另一个交点是F（2，2）；（1）观察图像，直接说出当时，x的值；（2）求证：CE=DF;（3）连接OE、OF，求S△OEF的面积.2ykxb14(0)yxx12yy拓展：如图，过点E(1,4)的直线分别交x轴、y轴于点D、C.若直线与双曲线的另一个交点是F点.（1）过点E、F分别作x轴、y轴的平行线，得到四边形OGAH,试探究四边形OGAH的形状并说明理由.（2）当四边形OGAH是正方形时，求证：OE=OF.2ykxb2ykxb14(0)yxx(3).当k发生变化时，OCE和△OFD的面积有着怎样的数量关系？谢谢