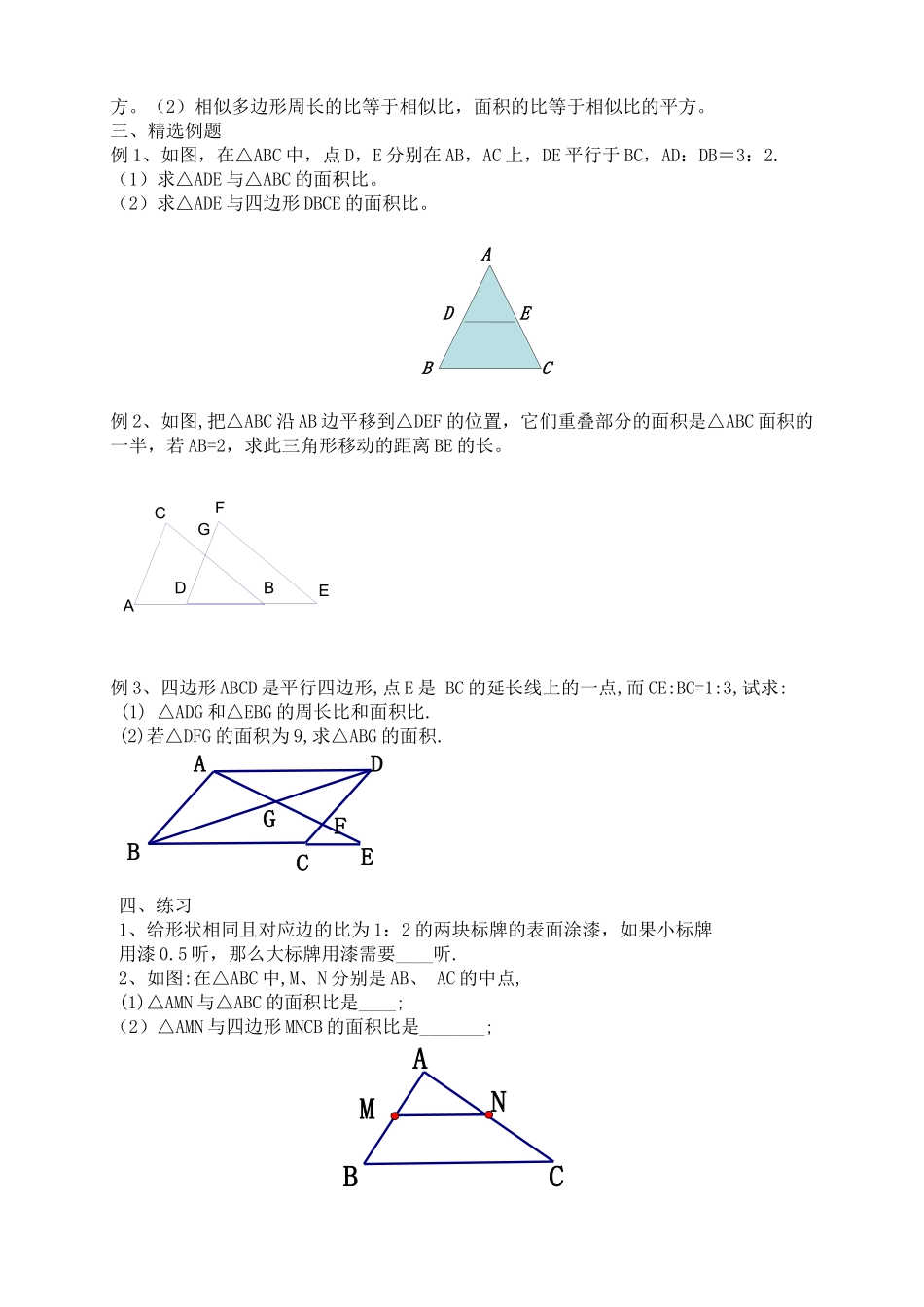
课题:相似三角形的性质(1)句容二中何昌荣教学目标:1.探索相似三角形、相似多边形的性质,会运用相似三角形、相似多边形的性质解决有关问题.2.通过实践与探索,得到相似三角形的周长比及面积比与相似比的关系,运用类比的方法得出相似多边形的周长比及面积比与相似比的关系.3.经历“探索—发现—猜想”,通过实际问题的研究,提高分析问题、解决问题的能力;4.通过实际问题的研究,发展从数学角度提出问题,解决问题的能力,增强用数学的意识.教学重点:相似三角形(多边形)的周长比及面积比与相似比的关系.教学难点:相似三角形(多边形)的面积比等于相似比的平方.教学过程:一、复习旧知1.什么样的三角形叫做相似三角形?2.相似三角形具有哪些性质?二、新知探索图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们相似吗?1、(2)与(1)的相似比=____,(2)与(1)的面积比=____;周长比=2、(3)与(1)的相似比=___,(3)与(1)的面积比=___;周长比=3、把相似比由数字换成字母K,那么周长的比、面积的比与相似比K又有什么关系呢?4、结论:相似三角形周长的比等于相似比,面积的比等于相似比的平方。5、已知:ΔABC∽ΔA´B´C´,''''''ABACBCABACBkC===求证:ΔABC的周长ΔA’B’C’的周长=ksABCsA´B´C´=k26、结论:(1)相似三角形周长的比等于相似比,面积的比等于相似比的平方。(2)相似多边形周长的比等于相似比,面积的比等于相似比的平方。三、精选例题例1、如图,在△ABC中,点D,E分别在AB,AC上,DE平行于BC,AD:DB=3:2.(1)求△ADE与△ABC的面积比。(2)求△ADE与四边形DBCE的面积比。CABDE例2、如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若AB=2,求此三角形移动的距离BE的长。GFEDCBA例3、四边形ABCD是平行四边形,点E是BC的延长线上的一点,而CE:BC=1:3,试求:(1)△ADG和△EBG的周长比和面积比.(2)若△DFG的面积为9,求△ABG的面积.DFGECBA四、练习1、给形状相同且对应边的比为1:2的两块标牌的表面涂漆,如果小标牌用漆0.5听,那么大标牌用漆需要____听.2、如图:在△ABC中,M、N分别是AB、AC的中点,(1)△AMN与△ABC的面积比是____;(2)△AMN与四边形MNCB的面积比是_______;ABCNM3、已知△ABC∽△A'B'C'其相似比是2,△ABC的周长是36,则A'B'C'的周长是________.4、小明把1米长的铜丝截成两段,用它们围成两个相似三角形且相似比为3:5,那么截成的两段铜丝的长度差是__________.5、已知两个相似多边形的相似比是4:5,周长的和是18cm,则两个多边形的周长分别是___________.6、如图,△ABC中,DEFGBC,AD=DF=FB,则S⁄⁄⁄⁄1:S2:S3=_________.S1S2S37、如图,DE∥BC,AD:DB=1:2,DC,BE交于点O,则△DOE与△BOC的周长之比是_________,面积比是_______。ODABCE五、小结---全等三角形与相似三角形性质比较面积比等于相似比的平方面积相等周长的比等于相似比周长相等对应角相等对应角相等对应边的比等于相似比对应边相等相似三角形全等三角形六、作业习题10.51、2、3