直线和平面平行的性质定理VIP免费

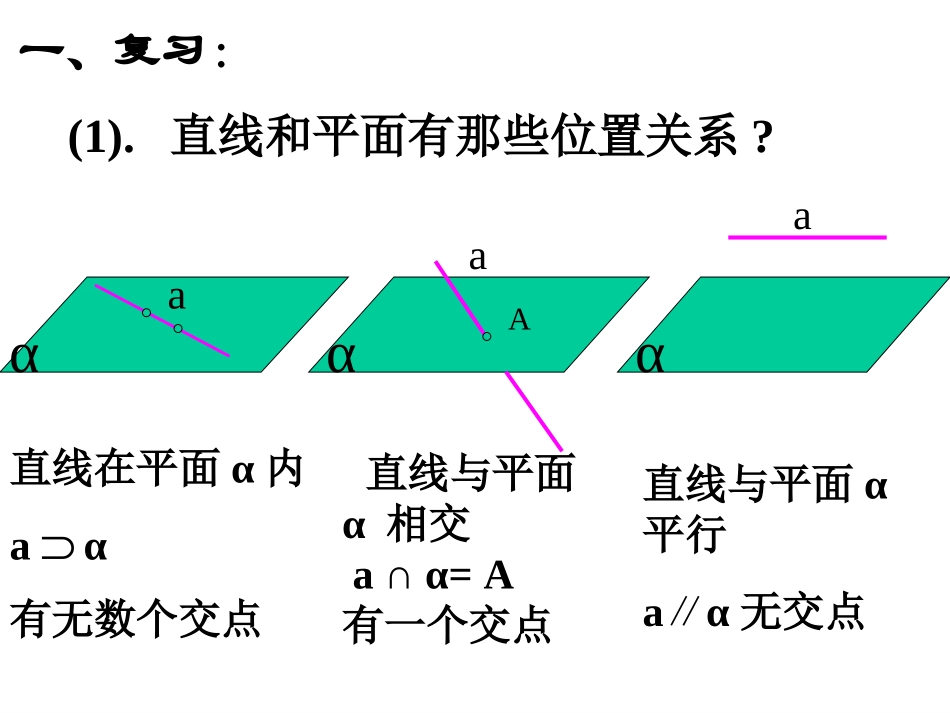
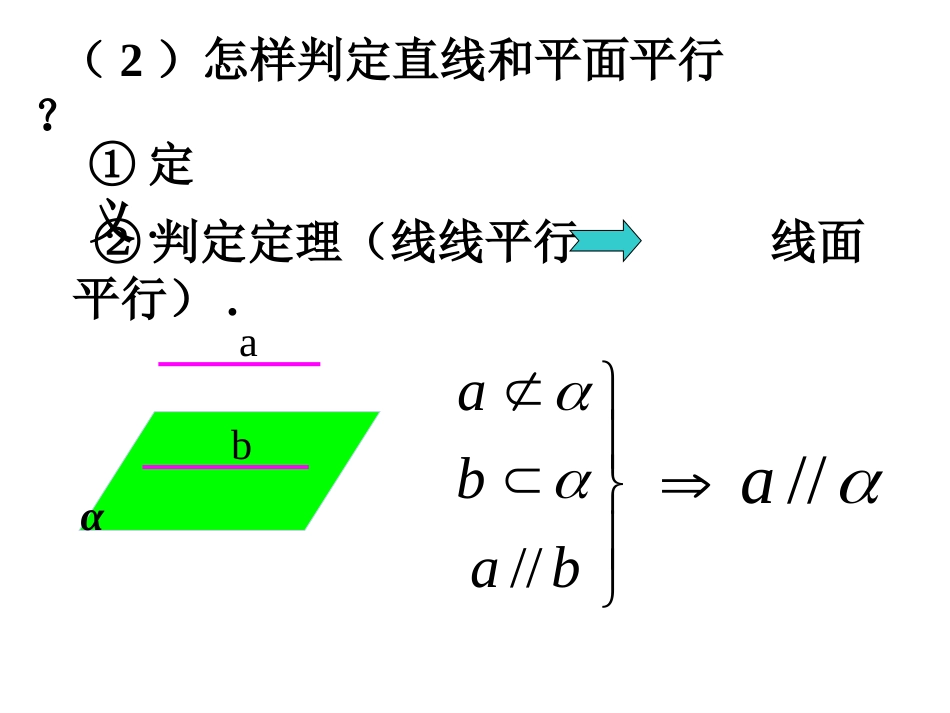
直线和平面平行性质定理1(1).直线和平面有那些位置关系?αa直线与平面α平行aα∥无交点直线在平面α内aα有无数个交点直线与平面α相交a∩α=A有一个交点αAa一、复习：aα（2）怎样判定直线和平面平行？①定义.//abab②判定定理（线线平行线面平行）.aαb//a复习2：线面平行的判定定理如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。baba∥baa∥注明：1、定理三个条件缺一不可。2、简记：线线平行，则线面平行。3、定理告诉我们：要证线面平行，需在平面内找一条直线，使线线平行。abca那么直线会与平面内那些线平行呢？本节课研究的内容思考：如果一条直线与平面平行，那么这条直线是否与这平面内的所有直线都平行？（3）如果一条直线和一个平面平行，那么这条直线和这个平面内的直线有怎样的位置关系？abαaαb（4）已知直线a∥平面α，如何在平面α内找出和直线a平行的一条直线？平行异面.交线为所求交，则作一平面与已知平面相过直线ala怎样作平行线？试用文字语言将上述原理表述成一个命题.a思考：教室内日光灯管所在直线与地面平行，如何在地面上作一条直线与灯管所在的直线平行？如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.上述定理反映了直线和平面平行的一个性质，其内容可简述为“线面平行，则线线平行”.线∥面线∥线判定直线与直线平行的重要依据。判定直线与直线平行的重要依据。图形图形作用：作用：符号语言符号语言::αβaba，//a，b//.ab关键：关键：寻找平面与平面的交线。寻找平面与平面的交线。返回如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。ba,,//aabab已知:直线求证:证明：//aa与没有公共点b又因为在内ab与没有公共点ab又与都在平面内且没有公共点//ab(1)“线面平行线线平行”(3)在有线面平行的条件或要证线线平行时，ml∥mll(2)线线平行线面平行babaaα∥证线面平行关键在于找线线平行（中位线、平行四边形）内容及目标：探究二（例3、例4、以及拓展）(1)直线与平面平行的性质；(2)如何由线面-----》线线；要求：（1）小组长首先安排任务先一对一分层讨论，再小组内集中讨论，AA力争拓展提升，BB、CC解决好全部展示问题。（2）讨论时，手不离笔、随时记录，争取在讨论时就能将错题解决，未解决的问题，组长记录好，准备展示质疑。（3）讨论结束时，将对各组讨论情况进行评价。合作探究高效展示展示问题位置展示例3后例4后拓展后目标：（1）规范认真，脱稿展示；（2）不但要展示解题过程，更重要的是展示规律方法、注意的问题、拓展；其他同学讨论完毕总结完善，A层注意拓展，不浪费一分钟；（3）小组长要检查落实，力争全部达标.目标：（1）先分析解题思路，再规范步骤，总结易错点，给展示题打分2--5（2）其它同学认真倾听、积极思考,重点内容记好笔记。有有不明白或有补充的要不明白或有补充的要大胆提出。大胆提出。（3）力争全部达成目标，A层多拓展、质疑,B层注重总结，C层多整理，记忆。科研小组成员首先要质疑拓展。让质疑成为最美丽的风景！让质疑成为最美丽的风景！高效点评展示问题位置展示点评例3后例4后拓展后例题讲解：abcαβ证明：过a作平面β交平面α于直线c aα∥∴ac∥又 ab∥∴bc∥∴bα.∥ bα,cα例1、已知直线a∥直线b，直线a∥平面α,bα求证：b∥平面αlαβ例2、如果两个相交平面分别经过两条平行直线中的一条，那么它们的交线和这两条直线平行.ab∴a∥l同理b∥l又 aα，平面α∩平面β=l已知:平面α∩平面β=l,aα,bβ,ab∥（如图）求证：a∥l,b∥l.故a∥l,b∥l.证明： ab∥，bβ，aβ∴aβ∥例3、有一块木料如图，已知棱BC平行于面A′C′．要经过木料表面A′B′C′D′内的一点P和棱BC将木料锯开，应怎样画线？所画的线和面AC有什么关系？ABCDABCDPEFA/D/B/C/ADCBP经典例题讲解解：（1）在平面内，过点P作直线EF...