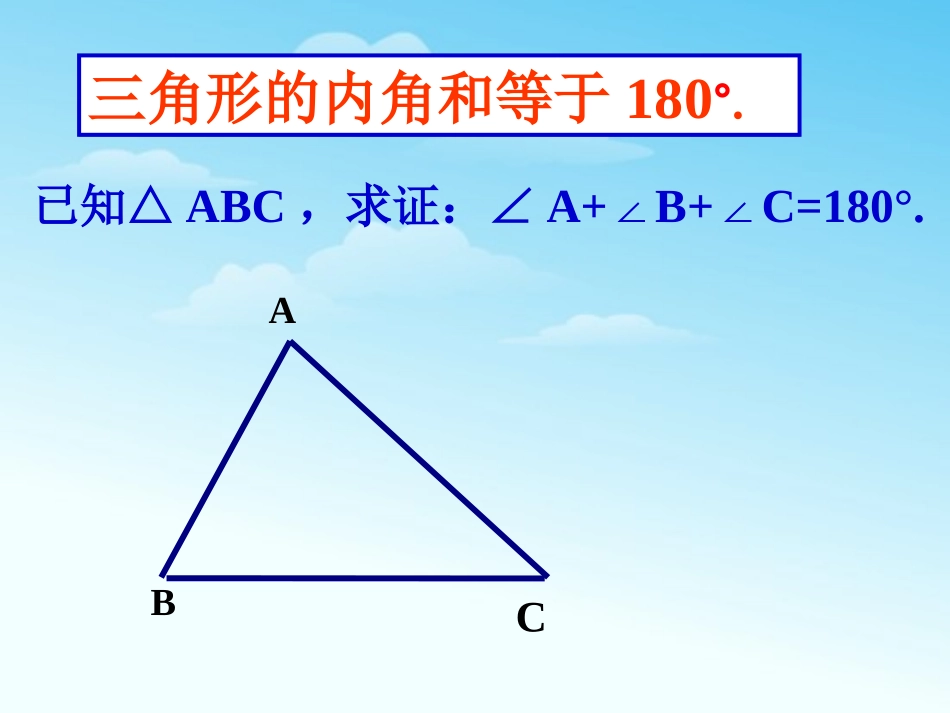
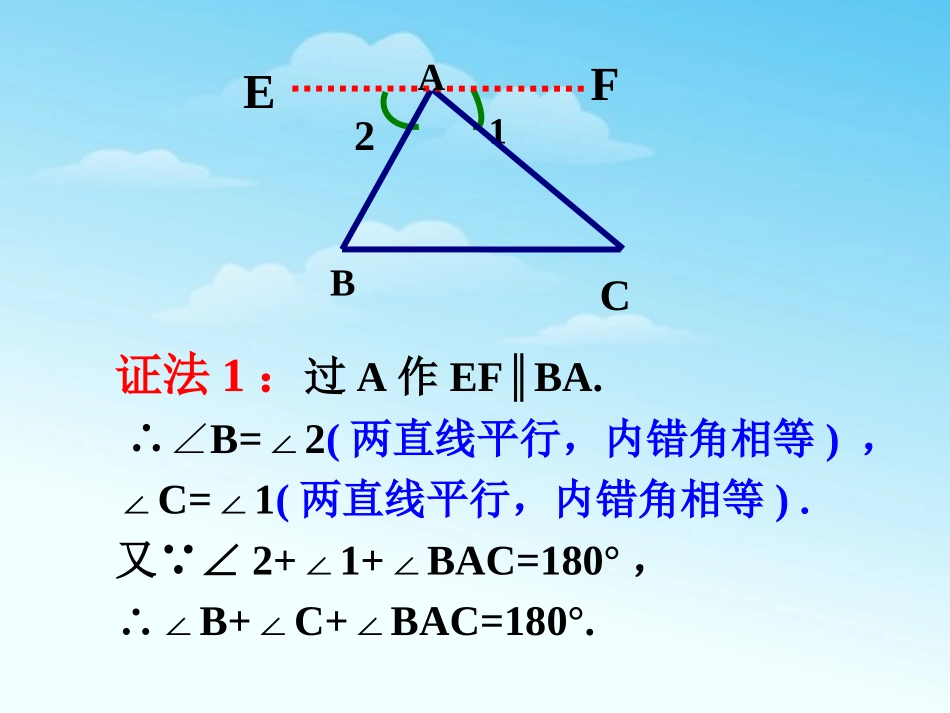
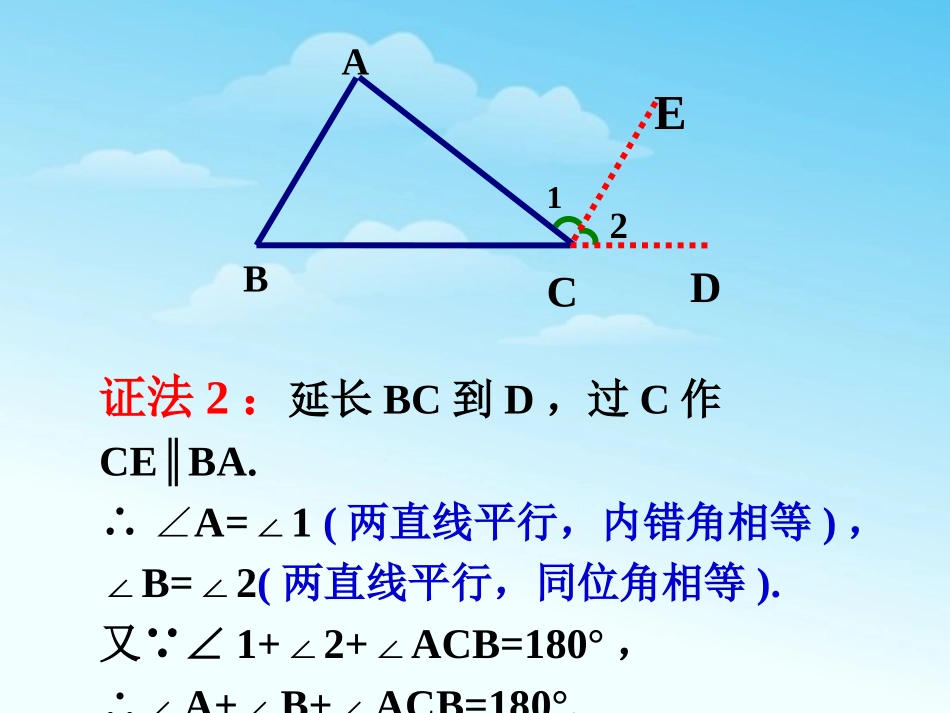
CBA三角形的内角和等于180°.已知△ABC,求证:∠A+B+C=180°.∠∠证法1:过A作EFBA.∥∴∠B=2∠(两直线平行,内错角相等),∠C=1∠(两直线平行,内错角相等).又∵∠2+1+BAC=180°∠∠,∴∠B+C+BAC=180°.∠∠F21ECBA证法2:延长BC到D,过C作CEBA.∥∴∠A=1∠(两直线平行,内错角相等),∠B=2∠(两直线平行,同位角相等).又∵∠1+2+ACB=180°∠∠,∴∠A+B+ACB=180°.∠∠21EDCBA证法3:过A作AEBC.∥∴∠B=BAE∠(两直线平行,内错角相等),∠EAB+BAC+C=180°∠∠(两直线平行,同旁内角互补).∴∠B+C+BAC=180°.∠∠CBEA在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.思路总结为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.