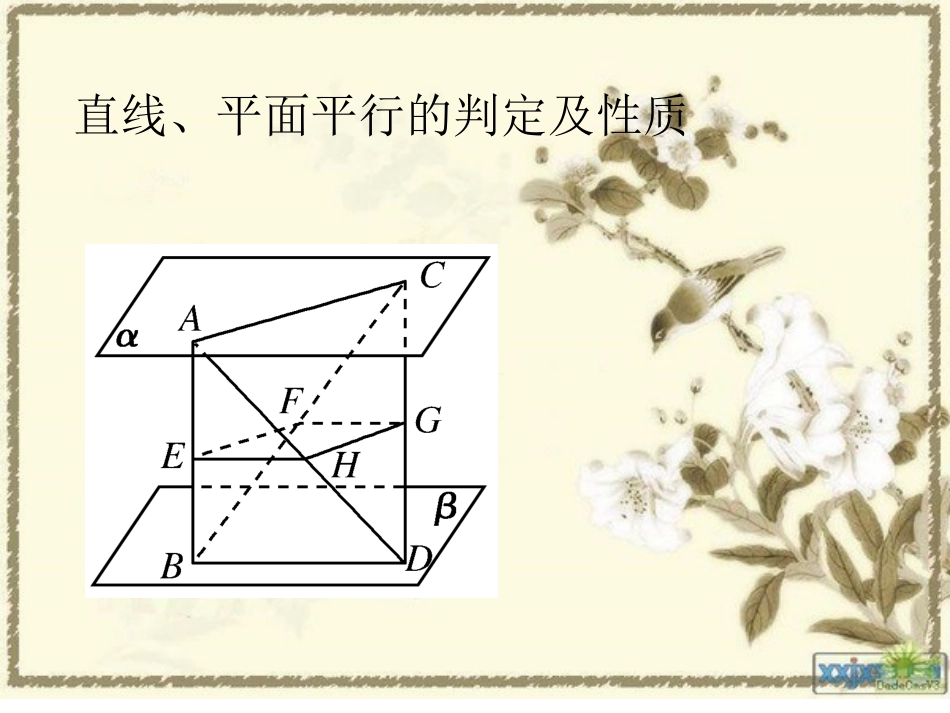
立体几何课件遂宁中学罗辉直线、平面平行的判定及性质直线、平面平行的判定及性质考题大攻略考前大冲关考向大突破2考向大突破1考向大突破3栏目顺序●请点击相关内容考向大突破一直线与平面平行的判定与性质例1如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,并且CM=DN.求证MN∥平面AA1B1B.证明:方法一:如图所示,作MEBC∥交BB1于E;作NFAD∥,交AB于F,连接EFEF结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引考向大突破一直线与平面平行的判定与性质例1如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,并且CM=DN.求证MN∥平面AA1B1B.方法二:过M作MQBB∥1交BC于Q,连接NQ.Q结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引归纳升华证明直线与平面平行常用的方法有以下三种:(1)利用定义(常用反证法).(2)利用判定定理:关键是找平面内与已知直线平行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线.(3)利用面面平行的性质:当两平面平行时,其中一个平面内的任一直线平行于另一平面.结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引变式训练1如图所示,在空间四边形ABCD中,截面EFGH为平行四边形,试证:BD∥平面EFGH,AC∥平面EFGH.证明: 截面EFGH为平行四边形,∴EHFG∥,根据直线与平面平行的判定定理知,EH∥平面BCD,又EH⊂平面ABD,平面ABD∩平面CBD=BD,根据直线与平面平行的性质定理知,BDEH∥,又EH⊂平面EFGH,BD⊄平面EFGH,因此,BD∥平面EFGH.同理,AC∥平面EFGH.结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引考向大突破二平面与平面平行的判定与性质例2在正方体ABCD-A1B1C1D1中,M,N,P分别是C1C,B1C1,C1D1的中点,求证:平面PMN∥平面A1BD.证明:方法一:如图,连接B1D1,B1C. P,N分别是D1C1,B1C1的中点,∴PNB∥1D1.又B1D1BD∥,∴PNBD.∥又PN⊄平面A1BD,∴PN∥平面A1BD.同理MN∥平面A1BD,又PN∩MN=N,∴平面PMN∥平面A1BD结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引考向大突破二平面与平面平行的判定与性质证明:方法二:如图,连接AC1,AC. ABCD-A1B1C1D1为正方体,∴ACBD.⊥又CC1⊥平面ABCD,∴AC为AC1在平面ABCD上的射影.∴AC1BD.⊥同理可证AC1A⊥1B,∴AC1⊥平面A1BD.同理可证AC1⊥平面PMN,∴平面PMN∥平面A1BD.例2在正方体ABCD-A1B1C1D1中,M,N,P分别是C1C,B1C1,C1D1的中点,求证:平面PMN∥平面A1BD.结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引归纳升华方法一利用了平面与平面平行的判定定理,关键是证明MN∥平面A1BD与PN∥平面A1BD,即用线线平行线面平行面面平行.⇒⇒方法二的证明利用了线面垂直的性质,需要注意证明线面垂直满足的条件“已知直线与平面内两条相交直线垂直”结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引变式训练2.如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,若Q是CC1上的中点.证明:平面D1BQ∥平面PAO.证明: Q为CC1的中点,P为DD1的中点,∴QBPA.∥ P,O分别为DD1,DB的中点,∴D1BPO.∥又 D1B⊄平面PAO,PO⊂平面PAO,QB⊄平面PAO,PA⊂平面PAO,∴D1B∥平面PAO,QB∥平面PAO,又D1B∩QB=B,D1B,QB⊂平面D1BQ,∴平面D1BQ∥平面PAO.结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引考向大突破三线面、面面平行的综合应用例3如图,已知αβ∥,异面直线AB,CD和平面α,β分别交于A,B,C,D四点,E,F,G,H分别是AB,BC,CD,DA的中点.求证:(1)E,F,G,H共面;(2)平面EFGH∥平面α.结束放映返回导航页考向大突破1考向大突破2考向大突破3考题大攻略考前大冲关栏目导引栏目导引考向大突破...