江苏科技大学附中高考数学一轮 推理与证明课时检测VIP免费

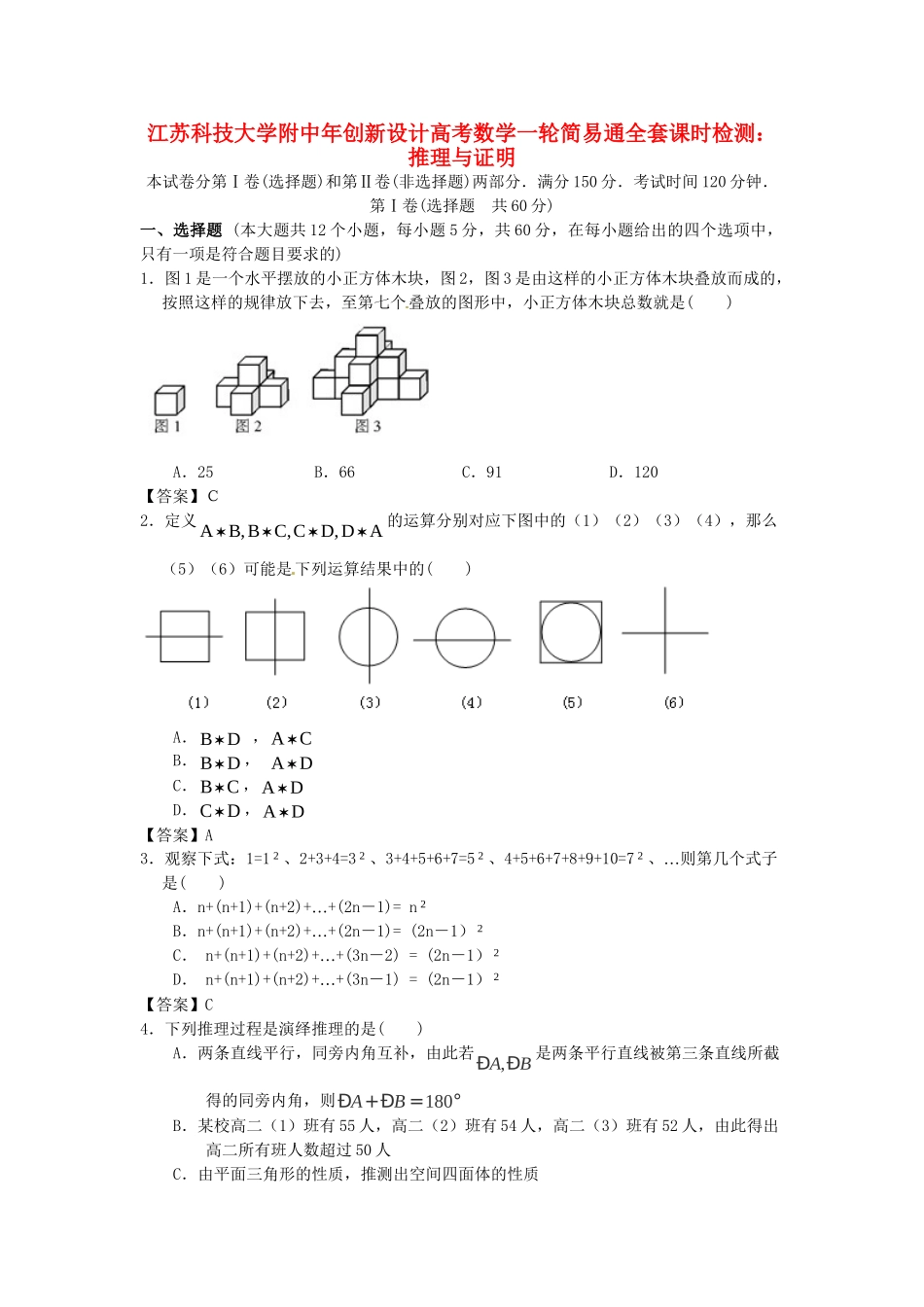
江苏科技大学附中年创新设计高考数学一轮简易通全套课时检测：推理与证明本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．图1是一个水平摆放的小正方体木块，图2，图3是由这样的小正方体木块叠放而成的，按照这样的规律放下去，至第七个叠放的图形中，小正方体木块总数就是()A．25B．66C．91D．120【答案】Ｃ2．定义AD,DC,CB,BA的运算分别对应下图中的（1）（2）（3）（4），那么（5）（6）可能是下列运算结果中的()A．DB，CAB．DB，DAC．CB，DAD．DC，DA【答案】A3．观察下式：1=12、2+3+4=32、3+4+5+6+7=52、4+5+6+7+8+9+10=72…、则第几个式子是()A．n+(n+1)+(n+2)+…+(2n－1)=n2B．n+(n+1)+(n+2)+…+(2n－1)=(2n－1）2C．n+(n+1)+(n+2)+…+(3n－2)=(2n－1）2D．n+(n+1)+(n+2)+…+(3n－1)=(2n－1）2【答案】C4．下列推理过程是演绎推理的是()A．两条直线平行，同旁内角互补，由此若,ABÐÐ是两条平行直线被第三条直线所截得的同旁内角，则180ABÐ+Ð=°B．某校高二（1）班有55人，高二（2）班有54人，高二（3）班有52人，由此得出高二所有班人数超过50人C．由平面三角形的性质，推测出空间四面体的性质D．在数列{}na中，1111,12()(2)1nnnaaana-==+³-，由此归纳出{}na的通项公式【答案】A5．若大前提是：任何实数的平方都大于0，小前提是：aR，结论是：20a，那么这个演绎推理出错在()A．大前提B．小前提C．推理过程D．没有出错【答案】A6．观察下列各式：1ba，322ba，433ba，744ba，1155ba，…，则1010ba()A．28B．123C．76D．199【答案】C7．已知2n且Nn，对2n进行如下方式的“分拆”：22→)3,1(，23→)5,3,1(，24→)7,5,3,1(，…，那么361的“分拆”所得的数的中位数是()A．19B．21C．29D．361【答案】A8．德国数学家洛萨·科拉茨1937年提出了一个猜想：任给一个正整数n，如果它是偶数，就将它减半；如果它是奇数，则将它乘3再加1，不断重复这样的运算，经过有限步后，一定可以得到1。如初始正整数为6，按照上述变换规则，得到一个数列：6，3，10，5，16，8，4，2，1。现在请你研究：如果对正整数n（首项），按照上述规则实施变换（1可以多次出现）后的第八项为1，则n的所有可能的对值为()A．2，3，16，20，21，128B．2，3，16，21C．2，16，21，128D．3，16，20，21，64【答案】A9．现有两个推理：①在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”；②由“若数列na为等差数列，则有15515211076aaaaaa成立”类比“若数列nb为等比数列，则有15152151076bbbbbb成立”，则得出的两个结论()A．只有①正确B．只有②正确C．都正确D．都不正确【答案】C10．对命题“正三角形的内切圆切与三边的中点”可类比猜想出：正四面体的内切球切与四面都为正三角形的什么位置？()A．各三角形内的点B．各正三角形的中心C．各正三角形的某高线上的点D．三条棱的中点【答案】B11．用数学归纳法证明(1)(2)()213(21)nnnnnn····，从k到1k，左边需要增乘的代数式为()A．21kB．2(21)kC．211kkD．231kk【答案】Ｂ12．已知f(x)=mxx33，在[0,2]上任取三个数a、b、c,均存在以f(a)、f(b)、f(c)为边的三角形，则m的范围为()A．m>2B．m>4C．m>6D．m>8【答案】C第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．给出下列四个结论：①命题“∃x∈R，x2－x>0”的否定是“∀x∈R，x2－x≤0”②“若am20时，f′(x)>0，g′(x)>0，则x<0时，f′(x)>g′(x)．其中正确结论的序号是____________．(填上所有正确结论的序号)【答案】①④14...