高考数学总复习 模块四 立体几何与空间向量 限时集训（十三）立体几何 理-人教版高三全册数学试题VIP免费

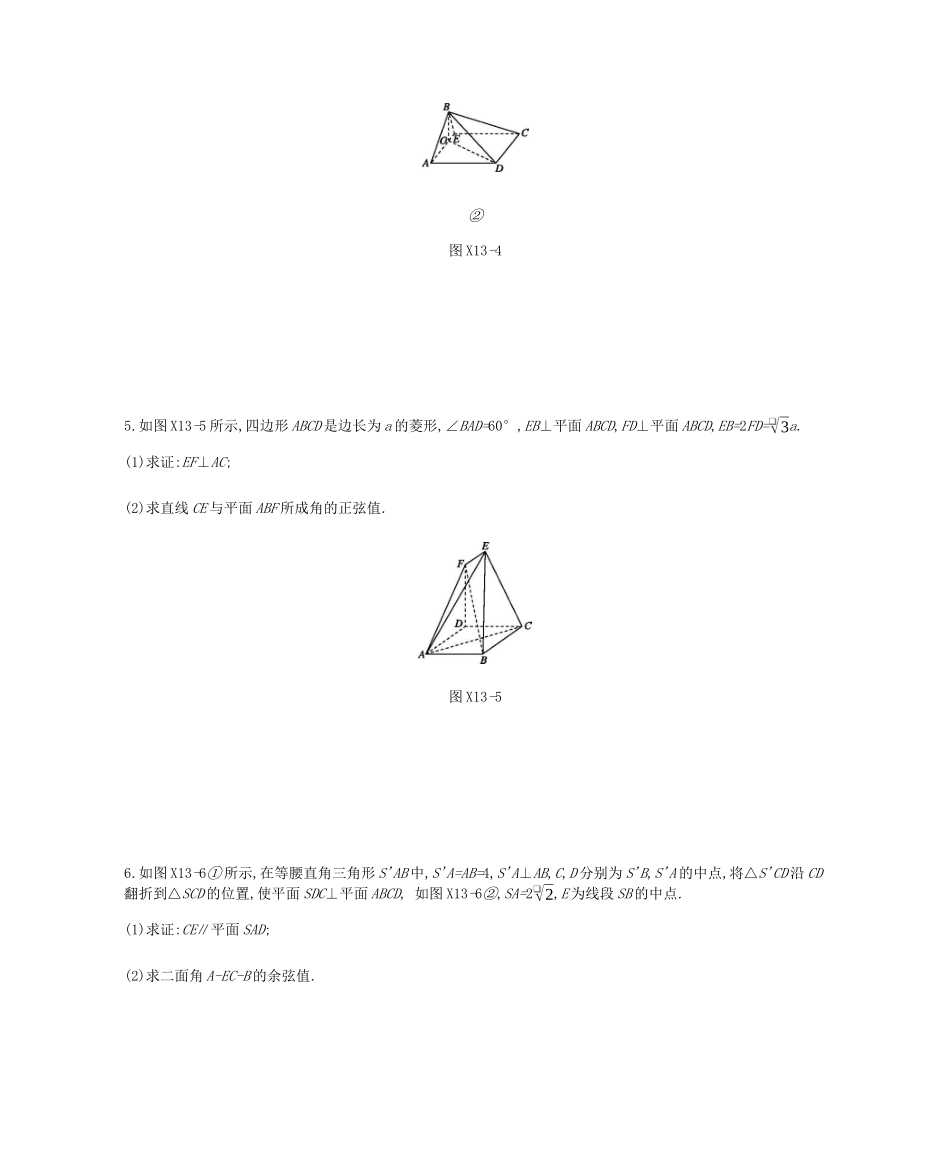
限时集训（十三）立体几何基础过关1.如图X13-1所示,在三棱柱ABC-A1B1C1中,△ABC和△AA1C均是边长为2的等边三角形,点O为AC的中点,平面AA1C1C⊥平面ABC.(1)证明:A1O⊥平面ABC;(2)求直线AB与平面A1BC1所成角的正弦值.图X13-12.在如图X13-2所示的几何体中,DE∥AC,AC⊥平面BCD,AC=2DE=4,BC=2,DC=1,∠BCD=60°.(1)证明:BD⊥平面ACDE;(2)求平面BCD与平面BAE所成二面角的正弦值.图X13-23.如图X13-3所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥平面ABCD,M为棱DD1的中点,N为棱AD的中点,Q为棱BB1的中点.(1)证明:平面MNQ∥平面C1BD;(2)若AA1=2AB,棱A1B1上有一点P,且⃗A1P=λ⃗A1B1(λ∈(0,1)),使得二面角P-MN-Q的余弦值为13❑√2163,求λ的值.图X13-34.如图X13-4①所示,四边形ABCD是一个直角梯形,∠ABC=∠BAD=90°,E为BC上一点,AE,BD相交于点O,AD=EC=3,BE=1,AB=❑√3.将△ABE沿AE折起,使平面ABE⊥平面ADCE,得到如图X13-4②所示的四棱锥B-AECD.(1)求证:CD⊥平面BOD;(2)求直线AB与平面BCD所成角的正弦值.①②图X13-45.如图X13-5所示,四边形ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=❑√3a.(1)求证:EF⊥AC;(2)求直线CE与平面ABF所成角的正弦值.图X13-56.如图X13-6①所示,在等腰直角三角形S'AB中,S'A=AB=4,S'A⊥AB,C,D分别为S'B,S'A的中点,将△S'CD沿CD翻折到△SCD的位置,使平面SDC⊥平面ABCD,如图X13-6②,SA=2❑√2,E为线段SB的中点.(1)求证:CE∥平面SAD;(2)求二面角A-EC-B的余弦值.①②图X13-6能力提升7.如图X13-7所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=AC=2,AD=2❑√2,PB=3❑√2,PB⊥AC.(1)求证:平面PAB⊥平面PAC.(2)若∠PBA=45°,试判断棱PA上是否存在与点P,A不重合的点E,使得直线CE与平面PBC所成角的正弦值为❑√33?若存在,求出AEAP的值;若不存在,请说明理由.图X13-78.如图X13-8所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AD∥BC,AB=BC=PA=1,AD=2,∠PAD=∠DAB=∠ABC=90°,点E在棱PC上,且CE=λCP(0<λ<1).(1)求证:CD⊥AE.(2)是否存在实数λ,使得二面角C-AE-D的余弦值为❑√105?若存在,求出实数λ的值;若不存在,请说明理由.图X13-8限时集训(十三)基础过关1.解:(1)证明: AA1=A1C,且O为AC的中点,∴A1O⊥AC,又平面AA1C1C⊥平面ABC,平面AA1C1C∩平面ABC=AC,且A1O⊂平面AA1C1C,∴A1O⊥平面ABC.(2)如图,连接OB,以O为原点,OB,OC,OA1所在直线分别为x,y,z轴建立空间直角坐标系,则O(0,0,0),A(0,-1,0),B(❑√3,0,0),A1(0,0,❑√3),C1(0,2,❑√3),∴⃗AB=(❑√3,1,0),⃗A1B=(❑√3,0,-❑√3),⃗A1C1=(0,2,0).设平面A1BC1的法向量为n=(x,y,z),则{n·⃗A1B=0,n·⃗A1C1=0,即{2y=0,❑√3x-❑√3z=0,令x=1,则y=0,z=1,∴n=(1,0,1).设直线AB与平面A1BC1所成的角为α,则sinα=|cos<⃗AB,n>|=|⃗AB·n||⃗AB||n|=❑√32×❑√2=❑√64,故直线AB与平面A1BC1所成角的正弦值为❑√64.2.解:(1)证明:在△BCD中,由余弦定理得BD2=22+12-2×1×2cos60°=3,所以BC2=BD2+DC2,所以BD⊥CD.又AC⊥平面BCD,所以AC⊥BD.因为AC∩CD=C,所以BD⊥平面ACDE.(2)易知DB,DC,DE两两垂直,所以以D为原点,DB,DC,DE所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系D-xyz,可得D(0,0,0),B(❑√3,0,0),C(0,1,0),E(0,0,2),A(0,1,4),则⃗BA=(-❑√3,1,4),⃗EA=(0,1,2).设n=(x,y,z)是平面BAE的法向量,则{n·⃗BA=−❑√3x+y+4z=0,n·⃗EA=y+2z=0,令z=❑√3,得n=(2,-2❑√3,❑√3).易知平面BCD的一个法向量为m=(0,0,1).设平面BCD与平面BAE所成二面角的平面角为θ,则|cosθ|=|n·m||n||m|=❑√3❑√19,从而sinθ=4❑√1919.3.解:(1)证明: M,Q分别为棱DD1,BB1的中点,∴MD􀱀BQ,∴四边形MQBD为平行四边形,∴MQ∥BD,又BD⊂平面C1BD,∴MQ∥平面C1BD.连接AD1, N为棱AD的中点,M为棱DD1的中点,∴MN∥AD1,又AD1∥BC1,∴MN∥BC1. BC1⊂平面C1BD,∴MN∥平面C1BD.又MN∩MQ=M,∴平面MQN∥平面C1BD.(2)由题意知DA,DC,DD1两两垂直,以D为原点,⃗DA,⃗DC,⃗DD1所在的方向分别为x,y,z轴的正方向,建立如图所示的空间直角坐标系,设AB=1,则A(1,0,0),N(12,0,0),M(0,0,1),Q(1,1,1),A1(1,0,2),B1(1,1,2),∴⃗A1B1=(0,1,0),⃗MN=...