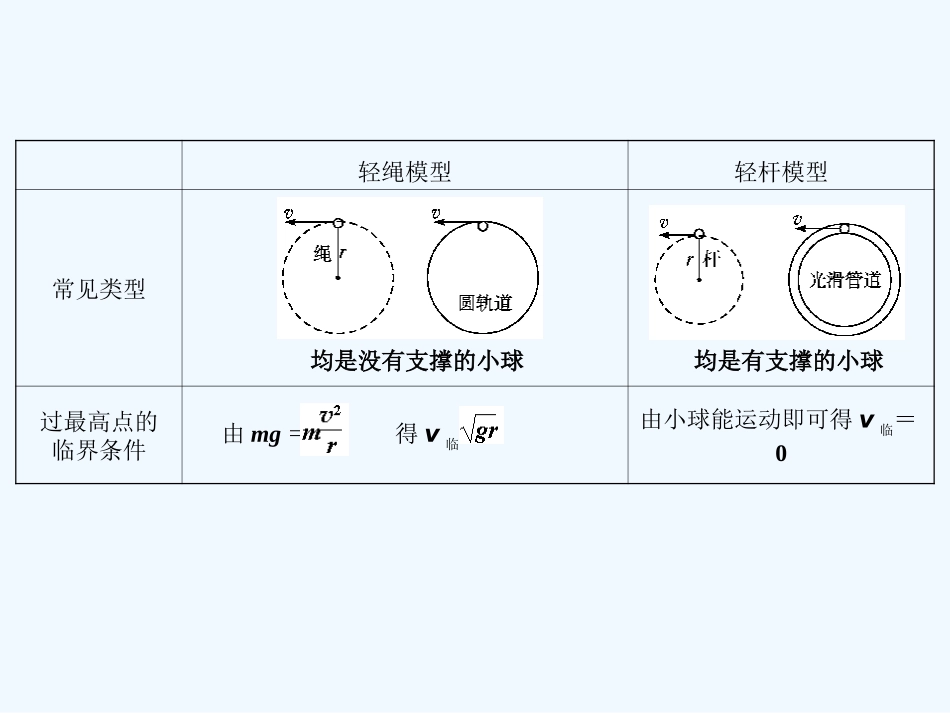
竖直面内圆周运动的临界问题分析对于物体在竖直面内做的圆周运动是一种典型的变速曲线运动,该类运动常有临界问题,并伴有“最大”“最小”“刚好”等词语,常分析两种模——型轻绳模型和轻杆模型,分析比较如下:第3课时专题圆周运动的临界问题轻绳模型轻杆模型常见类型过最高点的临界条件由mg=得v临=由小球能运动即可得v临=0均是没有支撑的小球均是有支撑的小球讨论分析(1)过最高点时,v≥,FN+mg=,绳、轨道对球产生弹力FN(2)不能过最高点v<,在到达最高点前小球已经脱离了圆轨道(1)当v=0时,FN=mg,FN为支持力,沿半径背离圆心(2)当0<v<时,-FN+mg=,FN背向圆心,随v的增大而减小(3)当v=时,FN=0(4)当v>时,FN+mg=,FN指向圆心并随v的增大而增大在最高点的FN图线取竖直向下为正向取竖直向下为正向1.如图4-3-1所示,汽车车厢顶部悬挂一个轻质弹簧,弹簧下端拴一个质量为m的小球,当汽车以某一速率在水平地面上匀速行驶时弹簧长度为L1;当汽车以同一速度匀速率通过一个桥面为圆弧形凸形桥的最高点时,弹簧长度为L2,下列答案中正确的是()A.L1=L2B.L1>L2C.L1