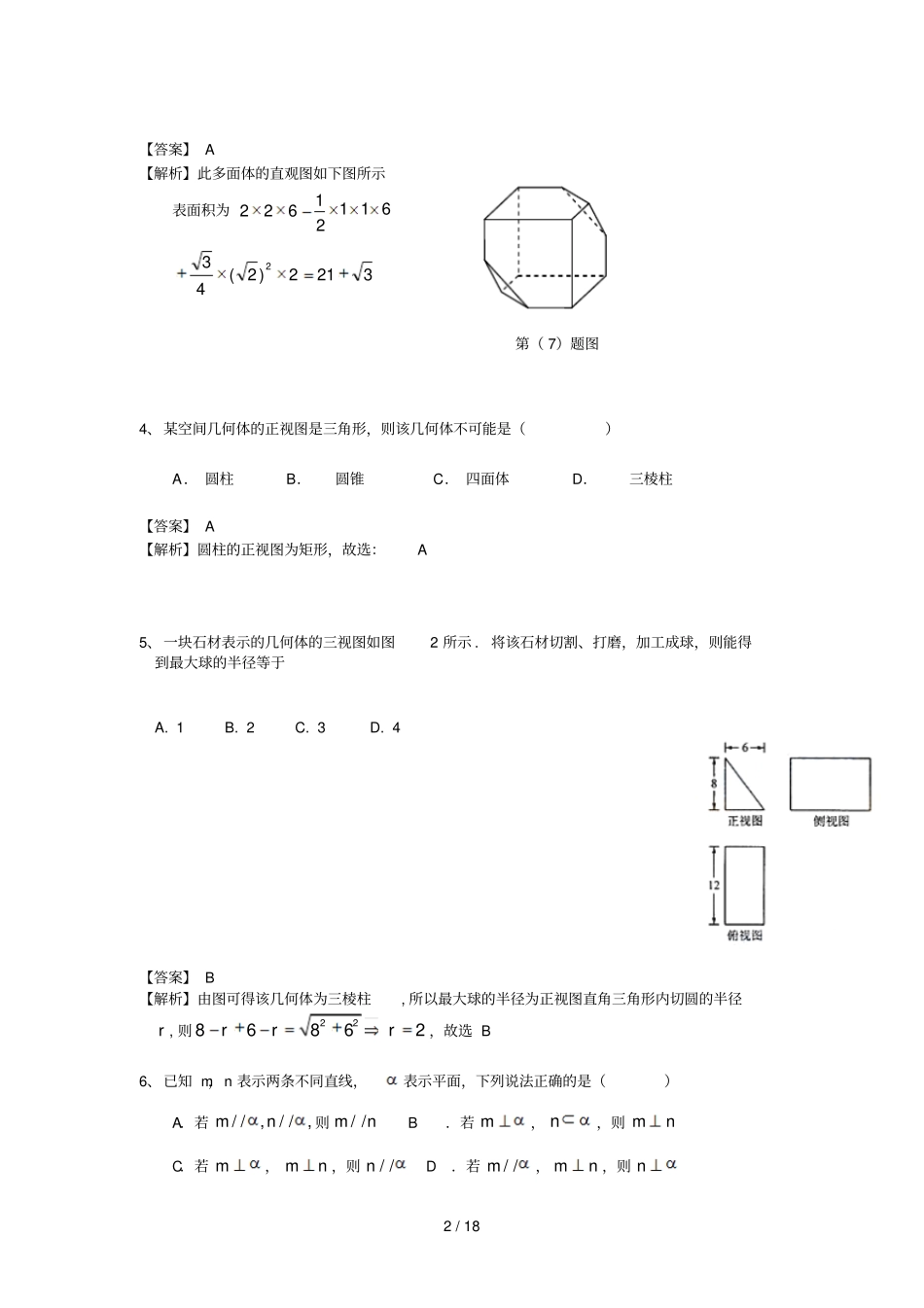
1/18高考理科数学立体几何考点练习1、已知底面边长为1,侧棱长为2则正四棱柱的各顶点均在同一个球面上,则该球的体积为()32.3A.4B.2C4.3D【答案】D【解析】Drrrr选解得设球的半径为.π3434V∴,1,4)2(11)2(,32222====++=π2、某几何体的三视图如下图所示,则该几何体的表面积为()A.54B.60C.66D.72【答案】B【解析】在长方体中构造几何体'''ABCABC,如右图所示,4,'5,'2,3ABAABBAC,经检验该几何体的三视图满足题设条件。其表面积'''''''''ABCACCAABBABCCBABCSSSSSS,3515615146022,故选择B3、一个多面体的三视图如图所示,则该多面体的表面积为(A)321(B)318(C)21(D)18俯视图左视图正视图3245C'B'A'CBA正(主)视图侧(左)视图11111111112/18【答案】A【解析】此多面体的直观图如下图所示表面积为611216223212)2(432第(7)题图4、某空间几何体的正视图是三角形,则该几何体不可能是()A.圆柱B.圆锥C.四面体D.三棱柱【答案】A【解析】圆柱的正视图为矩形,故选:A5、一块石材表示的几何体的三视图如图2所示.将该石材切割、打磨,加工成球,则能得到最大球的半径等于A.1B.2C.3D.4【答案】B【解析】由图可得该几何体为三棱柱,所以最大球的半径为正视图直角三角形内切圆的半径r,则2286862rrr,故选B6、已知m,n表示两条不同直线,表示平面,下列说法正确的是()A.若//,//,mn则//mnB.若m,n,则mnC.若m,mn,则//nD.若//m,mn,则n3/18【答案】B【解析】A.若m∥α,n∥α,则m,n相交或平行或异面,故A错;B.若m⊥α,n?α,则m⊥n,故B正确;C.若m⊥α,m⊥n,则n∥α或n?α,故C错;D.若m∥α,m⊥n,则n∥α或n?α或n⊥α,故D错.故选B7、正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A.814B.16C.9D.274【答案】A【解析】设球的半径为R,则 棱锥的高为4,底面边长为2,∴R2=(4﹣R)2+()2,∴R=,∴球的表面积为4π?()2=.故选:A8.如图,在正方体1111ABCDABCD中,点O为线段BD的中点。设点P在线段1CC上,直线OP与平面1ABD所成的角为,则sin的取值范围是A.3[,1]3B.6[,1]3C.622[,]33D.22[,1]3【答案】B【解析】直线OP与平面1ABD所成的角为的取值范围是111[,][,]22AOACOA,由于16sin3AOA,1163226sin23333COA,sin124/18所以sin的取值范围是6[,1]39、某几何体三视图如图所示,则该几何体的体积为()A.82B.8C.82D.84【答案】B【解析】由三视图知:几何体是正方体切去两个圆柱,正方体的棱长为2,切去的圆柱的底面半径为1,高为2,∴几何体的体积V=23﹣2××π×12×2=8﹣π.故选:B10、已知二面角l为060,AB,ABl,A为垂足,CD,Cl,0135ACD,则异面直线AB与CD所成角的余弦值为()A.14B.24C.34D.12【答案】B【解析】如图,过A点做AE⊥l,使BE⊥β,垂足为E,过点A做AF∥CD,过点E做EF⊥AE,连接BF, AB⊥l,∴∠BAE=60°,又∠ACD=135°,∴∠EAF=45°,在Rt△BEA中,设AE=a,则AB=2a,BE=a,在Rt△AEF中,则EF=a,AF=a,在Rt△BEF中,则BF=2a,∴异面直线AB与CD所成的角即是∠BAF,∴cos∠BAF===.5/1811、如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A.62B.42C.6D.4【答案】:C【解析】:如图所示,原几何体为三棱锥DABC,其中4,42,25ABBCACDBDC,24246DA,故最长的棱的长度为6DA,选C12、如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.1727B.59C.1027D.13【答案】C【解析】6/18..2710π54π34-π54π.342π944.2342π.546π96321Cvv故选积之比削掉部分的体积与原体体积,高为径为,右半部为大圆柱,半,高为小圆柱,半径加工后的零件,左半部体积,,高加工前的零件半径为==∴=?+?=∴=?=∴π13、直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成的角的余弦值为()A.110B.25C.3010D.22【答案】C【解析】..10305641-0||||θcos2-1-,0(2-1...