函数应用举例VIP免费

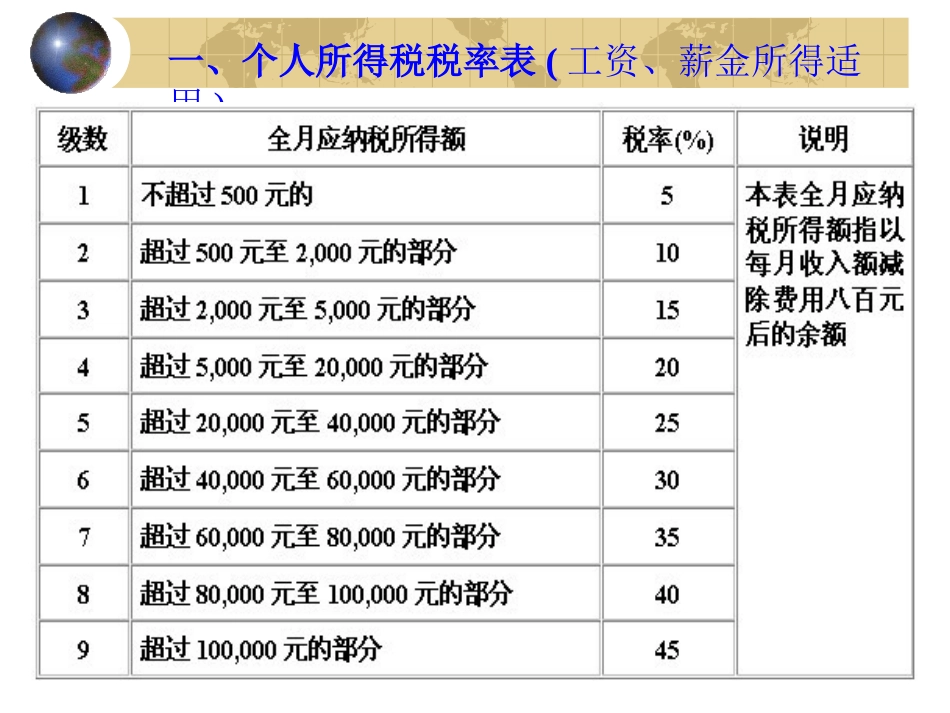
一、个人所得税税率表(工资、薪金所得适用)目的要求通过例题的学习,学会如何建立数学模型(函数关系式),帮助我们解决实际问题。通过例题的学习,学会如何建立数学模型(函数关系式),帮助我们解决实际问题。例1.建筑一个容积为8000m3,深为6m的长方体蓄水池,池壁的造价为a元/m2,池底的造价为2a元/m2,把总造价y(元)表示为底的一边长x(m)的函数。ABCB1C1A1D1D分析:思考下列问题:1.此题己知条件中出现了什么样的新概念丶新字母?它们的含义是什么?(长方体AC1丶蓄水池丶池壁(四周)丶池底ABCD丶造价丶底边长x丶总造价y。)2.在出现的新概念丶新字母中彼此之间有什么联系和制约?(长方体AC1的体积=池底面积(SABCD)高(AA1);池底面积=AB·BC=x·z;池壁面积=2SABB1A1+2SBCC1B1造价:1平方米所需的费用;总造价(y)=池底造价+池壁造价)3.要解决什么问题?(写出函数关系式)4.要求总造价,关键要解决什么量?(关键是建筑总量,即池底面和池壁面积)5.这个蓄水池有盖(封顶)吗?(无)解:设AB=x(m),BC=z(m)AA1=6(m)(即池深为6m)根据题意有:6xz=8000所以40003xZ=xzABCB1C1A1D1D池壁的造价为:池底的造价为:a(2x+2z)6=..40003x12a(x+),80003a]所以总造价为:.800062a=80003a40003xY=[12a(x+)+该例的启示:实际问题读懂问题将问题简单化数学建模解决问题基础过程关键目的例3.CDABO如图,有一块半径为R的半圆形钢板,计划剪成等腰梯形ABCD的形状,它的下底AB是圆O的直径,上底CD的端点在圆周上。写出这个梯形周长Y和腰长X间的函数关系式,并求出它的定义域。分析:思考下列问题1.此题已知条件中出现了什么样的新概念、新字母?它们的含义是什么?(钢板、梯形、半径R、直径AB、腰长x、周长y)2.在出现的新概念、新字母中彼此之间有什么联系和制约?(下底AB是圆O的直径、上底CD的端点在圆周上、周长y与下底AB(2R)、两腰长x以及上底CD有关)3.要解决什么问题?(写出函数解析式丶求出定义域)4.要写出周长y,关键解决什么量?(关键解决上底与腰长x、半径R的关系)CDABO解:如图,AB=2R,C、D在圆O上,E设腰长AD=BC=x,作DEAB垂足为E。连结BD,那么ADB是直角由此,RtADE与RtABD相似所以AD2=AEAB.即AE=x22R所以CD=AB-2AEx2R=2R-,所以周长Y满足关系式:x2R-+2x+4R即周长y和腰长x间的关系为y=Y=2R+2x+(2R-x2R)=x2R-+2x+4R因为ABCD是圆内接梯形,所以AD>0,AE>0,CD>0,X>0x22R>0x2R2R-->0解这个不等式组,得函数y的定义域为{x丨0