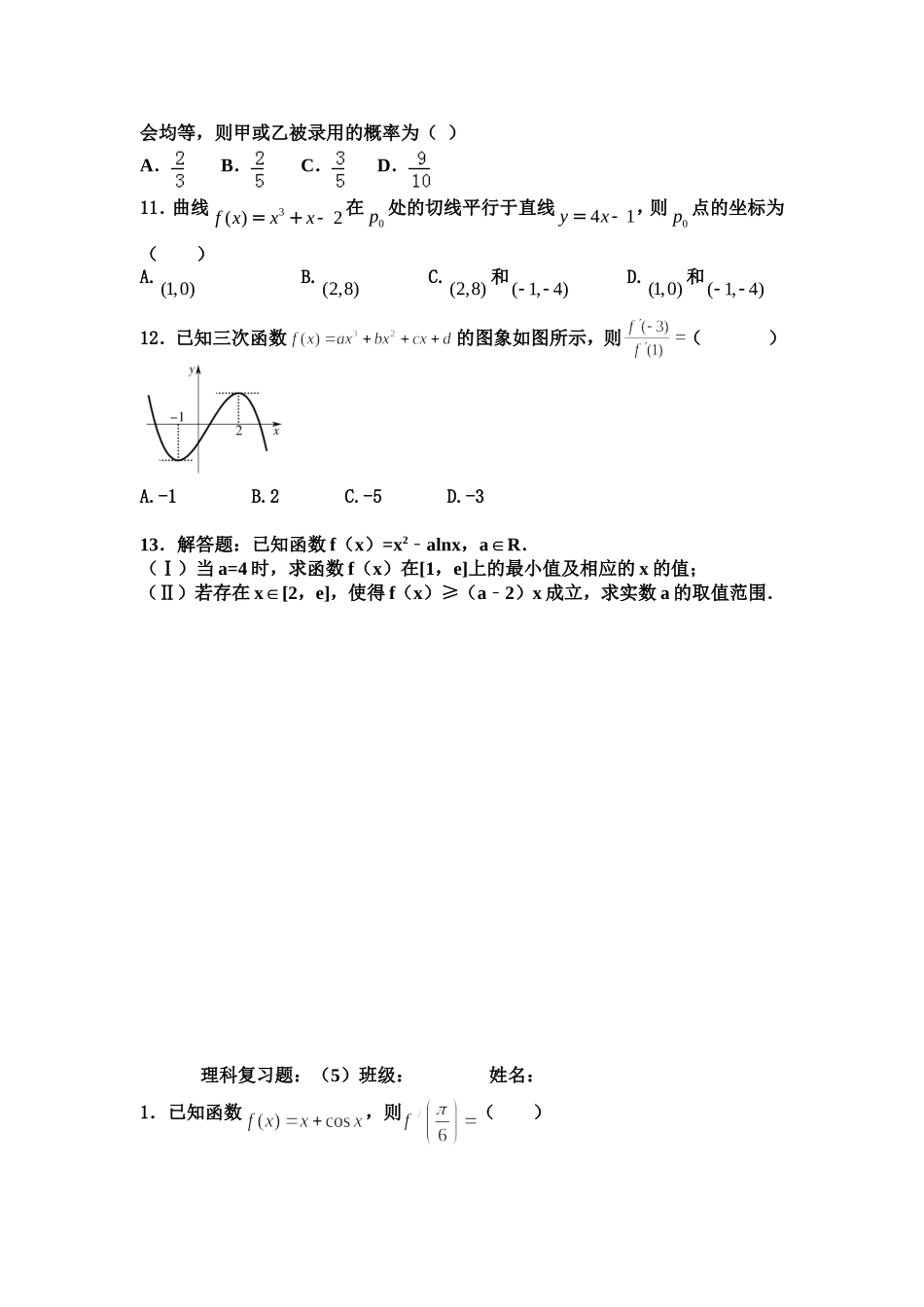
理科复习题:(4)班级:姓名:1.若曲线f(x)=x4-2x在点P处的切线垂直于直线x+2y+1=0,则点P的坐标为()A.(1,1)B.(1,-1)C.(-1,1)D.(-1,-1)2.设函数f(x)=+lnx,则()A.x=为f(x)的极大值点B.x=为f(x)的极小值点C.x=2为f(x)的极大值点D.x=2为f(x)的极小值点3.对任意的x∈R,函数f(x)=x3+ax2+7ax不存在极值点的充要条件是()A.0≤a≤21B.a=0或a=7C.a<0或a>21D.a=0或a=214.设x=-2与x=4是函数f(x)=x3+ax2+bx的两个极值点,则常数a-b的值为________.5.已知复数z满足z•(i1﹣)=2i,则z的共轭复数为()A.1iB﹣.1+iC.﹣1+iD.﹣1i﹣6.某班有4个空位,安排从外校转来的3个学生坐到这4个空位上,每人一个座位,则不同的坐法有()A.24种B.43种C.34种D.4种7.解答题:已知实数a>0,求函数f(x)=ax(x-2)2(x∈R)的单调区间.8.解答题:若函数f(x)=ax2+2x-lnx在x=1处取得极值.(1)求a的值;(2)求函数f(x)的单调区间及极值.9.设曲线y=x22x4lnx﹣﹣的一条切线的斜率小于0,则切点的横坐标的取值范围是()A.(﹣1,2)B.(﹣1,0)∪(2,+∞)C.(0,2)D.(0,+∞)10.若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为()A.B.C.D.11.曲线3()2fxxx=+-在0p处的切线平行于直线41yx=-,则0p点的坐标为()A.(1,0)B.(2,8)C.(2,8)和(1,4)D.(1,0)和(1,4)12.已知三次函数的图象如图所示,则()A.-1B.2C.-5D.-313.解答题:已知函数f(x)=x2alnx﹣,a∈R.(Ⅰ)当a=4时,求函数f(x)在[1,e]上的最小值及相应的x的值;(Ⅱ)若存在x∈[2,e],使得f(x)≥(a2﹣)x成立,求实数a的取值范围.理科复习题:(5)班级:姓名:1.已知函数,则()(A)(B)(C)(D)2.设(其中e为自然对数的底数),则的值为()A.43B.35C.37D.383.曲线上的点到直线的最短距离是()A.B.C.D.04.如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,则小正方形的边长为时,盒子容积最大?。5.点P是曲线上任意一点,则点P到直线的距离的最小值是6.若函数在区间内是增函数,则实数的取值范围是()A.B.C.D.7.曲线:在点处的切线恰好经过坐标原点,则曲线直线,轴围成的图形面积为()A.B.C.D.8.函数xexy)3(2的单调递增区间是()A.)0,(B.),0(C.)1,3(D.),1()3,(和9.解答题:已知函数在区间,上有极大值.(1)求实常数m的值.(2)求函数在区间,上的极小值.10.已知函数32()fxxaxbxc在23x与1x时都取得极值(1)求,ab的值与函数()fx的单调区间(2)若对[1,2]x,不等式2()fxc恒成立,求c的取值范围理科复习题:(6)班级:姓名:1.某单位安排7位员工在10月1日至7日值班,每天安排1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有()A504种B960种C1008种D1108种2.将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴亚运会的四个不同场馆服务,不同的分配方案有种(用数字作答).3.已知为一次函数,且,则=_______..4.复数=,则是()A.25B.5C.1D.75.直线与函数的图像有三个相异的交点,则的取值范围为()A.B.C.D.6.已知i是虚数单位,若复数(1i)(2i)a是纯虚数,则实数a等于.7.复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限8.计算等于()A.B.C.D.9.曲线与围成的图形的面积为()A.B.C.D..10.5位志愿者和他们帮助2位老人排成一排照相,要求这2位老人相邻,但不排在两端,则不同排法有()种A.1440B.960C.720D.48011.甲乙两人从4门课程中选修2门,则甲乙所选的课程中至少有1门不相同的选法共有()种A.6B.12C.30D.3612.求曲线,所围成图形的面积.13.()A、iB、iC、1D、114.解答题;已知函数:f(x)=x3+ax2+bx+c,过曲线y=f(x)上的点P(1,f(1))的切线方程为y=3x+1(1)y=f(x)在x=-2时有极值,求f(x)的表达式;(2)函数y=f(x)在区间[-2,1]上单调递增,求b的取值范围....