27.2.1-相似三角形的判定(第1课时)VIP免费

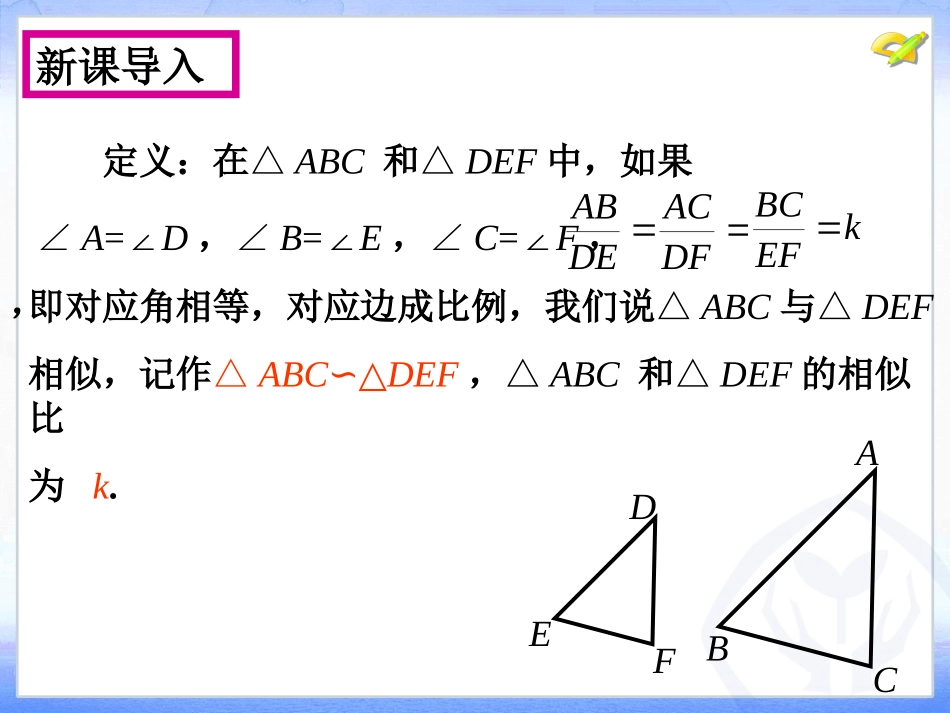
27.2.1相似三角形的判定九年级下册即对应角相等，对应边成比例，我们说△ABC与△DEF相似，记作△ABC∽△DEF，△ABC和△DEF的相似比为k.∠A=∠D，∠B=∠E，∠C=∠F，，新课导入DFACDEABkEFBCABCEDF定义：在△ABC和△DEF中，如果学习三角形全等时，我们知道，除了可以验证所有的角和边分别相等来判定两个三角形全等外，还有判定的简便方法（SSS，SAS，ASA，AAS）．类似地，判定两个三角形相似时，是不是也存在简便的判定方法呢？新课导入问题如图，任意画两条直线a，b，再画三条与a，b都相交的平行线l1，l2，l3．探究l1，l2，l3在直线a，b上截得的线段有什么关系．知识讲解l3l1l2ABDEFHab动画演示平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例．说明：①定理的条件是“两条直线被一组平行线所截”；②是“对应线段成比例”，注意“对应”两字．FHEFBDABEFFHABBD知识讲解l3l1l2ABDEFHab（=），左上左下右上右下（=）．左下左上右下右上如图l1∥l2∥l3，试根据图形写出成比例线段．l3abl1l2ABCDEF知识讲解EFDEBCABDEEFABBCDFDEACABDEDFABACDFEFACBCEFDFBCAC．，，，，，l2l3结论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．l1l3lll'ABCDEl2知识讲解ABCDEl1ll'A：（）B：（）C：（）D：（）ABCDE3．如图，DE∥BC，判断下列各式是否正确：迁移运用，拓展新知ACAEABADCEAEBDADABAEACADACABAEAD思考：如图，在△ABC中，DE∥BC，DE分别交AB，AC于点D，E，△ADE与△ABC有什么关系？迁移运用，拓展新知ADBEC探究、分析、证明、结论巩固练习，应用新知教材第31页第1、2题1．三角形相似的定义：归纳小结，反思提高平行于三角形一边的直线截其他两边（或两边延长线），所得的对应线段的比相等．2．平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例三个角分别相等，三条边成比例的两个三角形相似．3.判定三角形相似的定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。