正弦定理、余弦定理的应用VIP免费

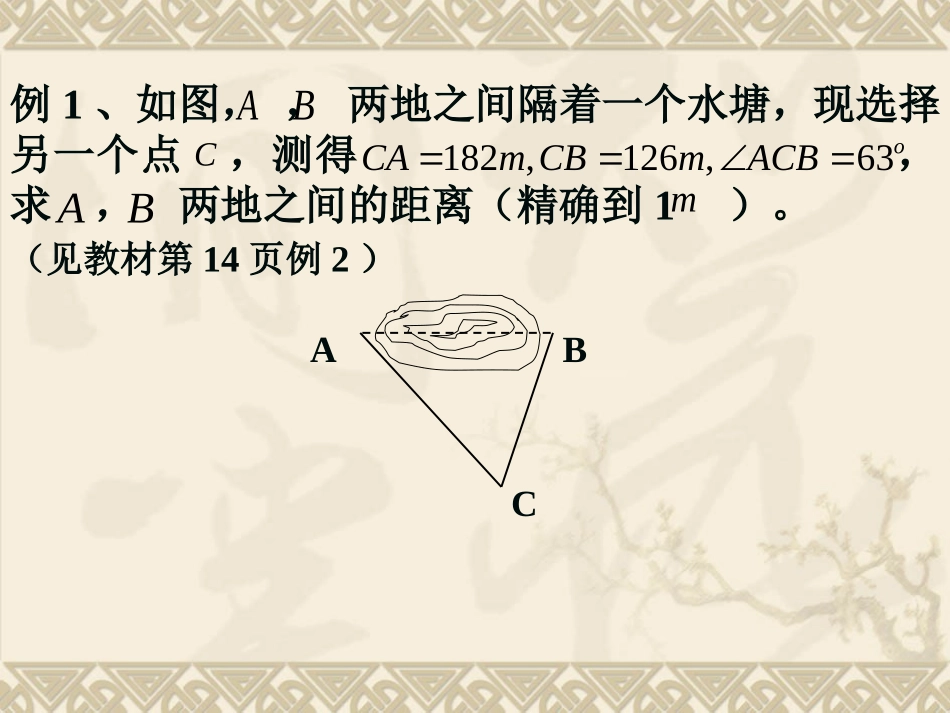
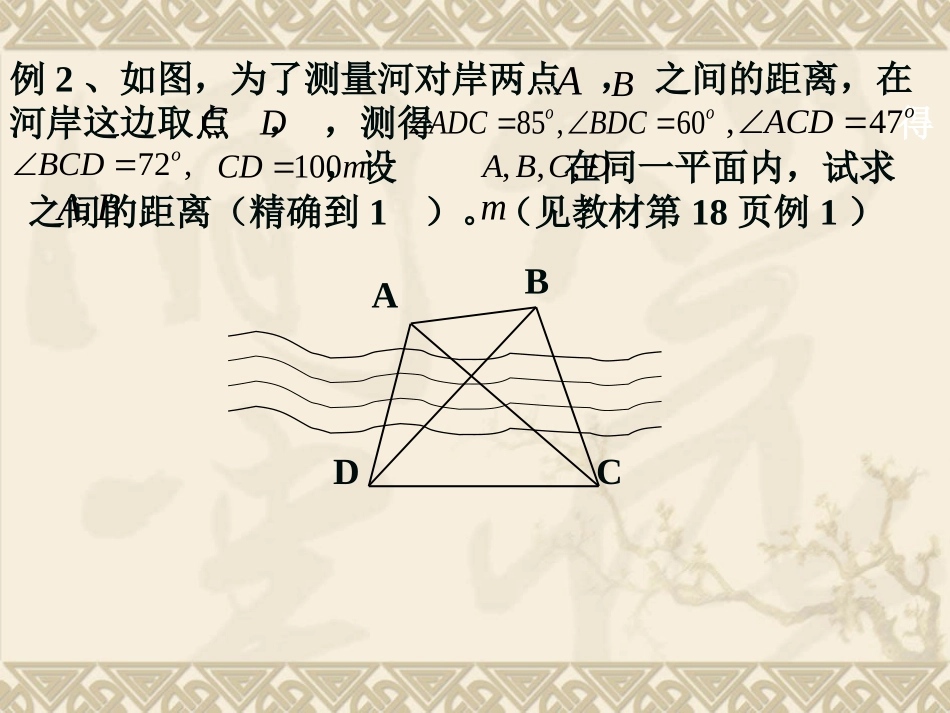
例1、如图，，两地之间隔着一个水塘，现选择另一个点，测得，求，两地之间的距离（精确到1）。ABC182,126,63oCAmCBmACBABm（见教材第14页例2）ABCACBDAB,AB例2、如图，为了测量河对岸两点，之间的距离，在河岸这边取点，，测得得，设在同一平面内，试求之间的距离（精确到1）。（见教材第18页例1）CD85,60ooADCBDC100CDm,,,ABCDm,47oACD72,oBCD小结：解三角形在测量中有着广泛应用，求，间距离的三种常见情形。ABACBaABCACBD（1）两点间不可通又不可视（2）两点间可视但不可达（3）两点都不可达例3、如图，某人在高出海面600m的山上P处，测得海面上的航标A在正东方向，俯角为，航标B在南偏东，俯角为，求这两个航标间的距离。（见教材第20页练习4）306045ACPB600例4、作用于同一点的三个力平衡。已知，与之间的夹角是，求的大小与方向（精确到）。（见教材第19页例3）123,,FFF1230,50FNFN1F2F60o3F0.1o1F3F2FO解有关斜三角形应用题的一般步骤：（1）准确理解题意，弄清已知和所求；（2）根据题意，画出示意图；（3）分析与研究一个或几个三角形；（4）正确运用正、余弦定理有序的求解。（5）回答实际问题关键：将实际问题转化为数学问题。课堂总结:ACBDN例5、在长江某渡口处，江水以的速度向东流。一渡船在江南岸的码头出发，预定要在后到达江北岸码头（如图所示）。设为正北方向，已知码头在码头的北偏东，并与码头相距。该渡船应按什么方向航行？速度是多少？（角度精确到，速度精确到）？（见教材第15页例4）5/kmhA0.1hBAN�BA15oA1.2km0.1o0.1/kmh例6、如图，某渔轮在航行中不幸遇险，发出呼救信号。我海军舰艇在A处获悉后，测出该渔轮在方位角为，距离为10nmile的C处，并测得渔轮正沿方位角为的方向，以9nmile/h的速度向小岛靠拢。我海军舰艇立即以21nmile/h的速度前去营救。求舰艇的航向和靠近渔轮所需的时间（角度精确到，时间精确到1min）。（见教材第18页例2）注：方位角是从指北方向顺时针旋转到目标方向线的角。451050.1oABC北北例7、如图，半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一点，以AB为一边作等边三角形ABC。问：点B在什么位置时，四边形OACB面积最大？（见教材第19页例4）例8、如图，有两条相交成角的直路，，交点是O，甲、乙分别在OX,OY上，起初甲离O点3km，乙离O点1km。后来甲沿的方向，乙沿的方向，同时用4km/h的速度步行。(见教材第21页第7题)（1）起初两人的距离是多少？（2）h后两人的距离是多少？（3）什么时候两人的距离最短？60'XX'YY'XX'YYt甲乙X'XY'Y