1.2定积分VIP免费

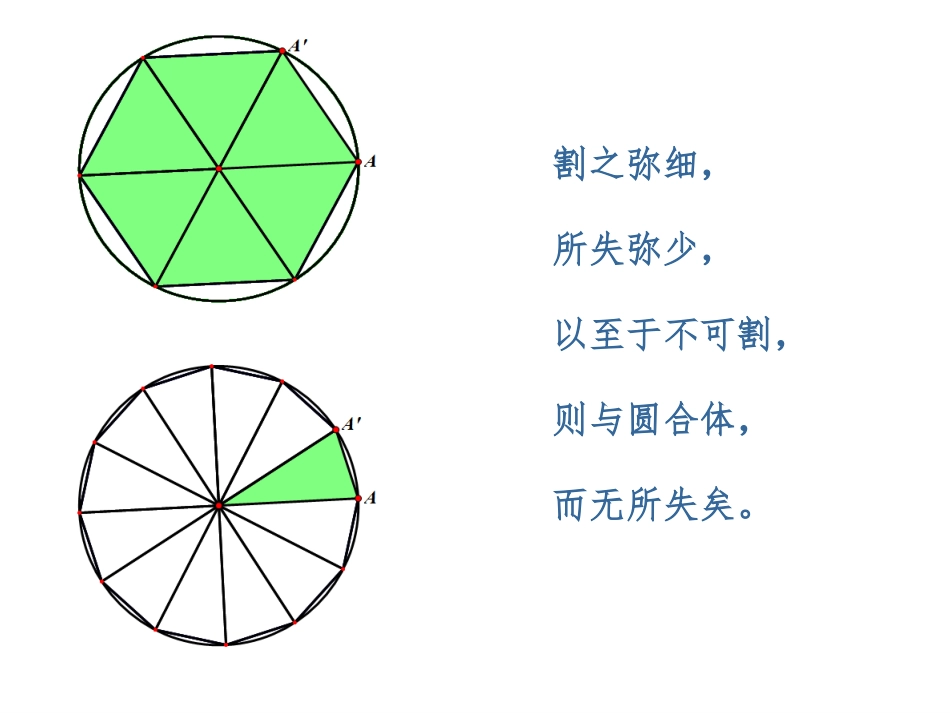
定积分的概念（北师大版）高中数学选修2-2第四章定积分§4.1•公元3世纪我国魏晋时期大数学家刘徽，用“割圆术”求出了圆的面积，从而得到了π的近似值。割之弥细，所失弥少，以至于不可割，则与圆合体，而无所失矣。abxyo?A原型一（求曲边梯形的面积）一、抽象定积分概念现实原型)(xfy曲边梯形由连续曲线轴与两直线,所围成.()(()0),yfxfxxxaxb将曲边梯形的底，即[a,b]进行分割(用垂直于x轴的直线).第一步分割；第一步分割；曲边梯形的面积的解决思路：abxyo)(xfyix1x1ix1nx2x记1.iiixxx第二步近似第二步近似abxyo)(xfy用矩形面积近似用矩形面积近似小曲边梯形面积小曲边梯形面积()if高底ix1x1ix1nx2xix小曲边梯形面积iSi().iiiSfxabxyo)(xfyix1x1ix1nx2x第三步求和；第三步求和；i矩形面积和与曲边梯形面积不相等有误差有误差121nn11().nniiiiiSfx将每个小曲边梯形的面积都用矩形近似，并将所有的小矩形面积加起来.第四步取极限.第四步取极限.当对曲边梯形底的分割越来越细时，矩形面积之和越近似于曲边梯形面积.abxyo)(xfy0,1,2,,ixinmax{}0ixiniixfA)(lim10abxyo?A)(xfy解决此问题的步骤：1）分割；2）近似；3）求和；4）取极限；iniixfA)(lim102）近似；3）求和；2）近似；4）取极限；3）求和；2）近似；2）近似；3）求和；2）近似；4）取极限；3）求和；2）近似；2）近似；3）求和；2）近似；4）取极限；3）求和；2）近似；2）近似；3）求和；2）近似；原形二（变速直线运动的路程）4）取极限；1）分割；2）近似；3）求和；设某物体做直线运动，已知速度，求该物体在运动时间[0,2]内所行使的路程s.t0tv12t练习：求函数与x轴，直线x=0，x=1所围成曲边梯形的面积..2)(xxf01xy解析：按求曲边梯形面积的四步曲来解答解：1）分割：将[0,1]区间等分成n分，则每个子区间依次为：],1[],1[]2,1[]1,0[nnnnnininnn、、、2）近似：nnixfSiii1)(223）求和：)21(1)1(2222221221nnnnnnniSAniniiniiSA16)12)(1(1)321(11322222nnnnnnn4)取极限：6)12)(1(1limlim31nnnnSAnniin2226132lim6)12)(1(1limnnnnnnnn31)612131(lim2nnn下一页1.曲边梯形的面积iniintS1)(liminiixfA10)(lim2.变速直线运动的路程变力沿直线做功、曲线的弧长等定积分iniixfA10)(lim012111111()[,],...[,][,](1,2,...),(1,2,...,).,=max{}0().nniiiiiiiiinniifxabaxxxxxbabnxxixxxinxxfxAAf设是定义在区间上的连续函数用点将区间任意分割成个子区间这些子区间及其长度均记作在每一子区间上任取一点只要时，总趋于确定的极限则称此极限为函数01()[,]().()lim()banbiiaixabfxdxfxdxfx在区间上的定积分，记作即二、定积分的定义定义被积函数被积表达式[,]ab为积分区间积分上限积分下限1(,max{}0,]),()[,niiiifxaxnxfb的极限存如果当同时最大子区间的长度时和式则称在区间在上可积.1(0)()lim()nbiianifxxfxd积分变量积分和()fxx即作业：用定义法求下列定积分练习2：计算定积分dxx213练习1：计算定积分dxx20)23(