8.3正态分布曲线VIP免费

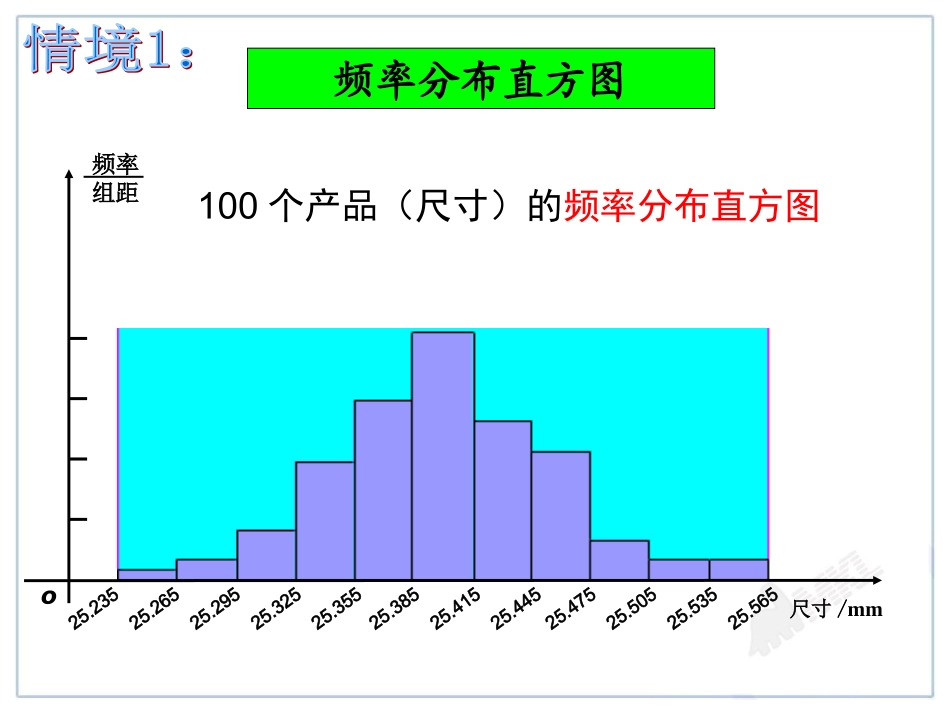
2.42.4正态分布正态分布重庆市两江中学校邓莉娅100个产品（尺寸）的频率分布直方图25.23525.29525.35525.41525.47525.535尺寸/mm频率组距25.26525.32525.38525.44525.50525.565o频率分布直方图产品内径尺寸/mm频率组距o200个产品（尺寸）的频率分布直方图频率分布直方图产品尺寸/mm频率组距o总体密度曲线当样本容量无限大,分组的组距无限缩小产品尺寸/mm频率组距o总体密度曲线在一块木板上固定很多平行且错开的圆柱形小木块，小木块之间留有适当的空隙作为通道。小球从最上方的通道口落下，在下落过程中会与层层小木块碰撞，最后掉入高尔顿板下方的某一球槽内。你见过高尔顿钉板吗？0132456频率组距789球槽编号根据高尔顿板的模型可以画出如下的频率分布直方图频率组距球槽编号频率组距球槽编号总体密度曲线频率组距球槽编号总体密度曲线这条曲线就是（或近似地是）下列函数的图像,,21222xexfx其中实数μ和σ(σ>0)为参数,我们称f(x)的图像为正态分布密度曲线，简称正态曲线。1.1.正态曲线的定义正态曲线的定义标准差：数学期望正态曲线,,21222xexfx的意义参数反映随机变量取值的平均水平，x=是图像的对称轴。参数是位置参数。正态曲线,,21222xexfx参数反映随机变量的集中与分散的程度，即标准差。参数是形状参数。由图象可以知道(1)越小，图象越“高瘦”.(2)越大，图象越“矮胖”.的意义(1)曲线位于x轴上方，与x轴不相交；(2)曲线是单峰的，中间高，两头低，关于直线x=μ对称；(3)曲线在x=μ处达到峰值;(4)曲线中s越小，图像越瘦高，s越大，图像越矮胖；(5)曲线与x轴之间的面积为1.212.2.正态曲线的特点正态曲线的特点课堂练习下列三个正态总体的函数表达式，请找出其均值μ和标准差σ（1）2221xexf（2）812221xexf（3）21222xexf1,02,15.0,1叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫叫()fxdxxfbXaPba)(.几何意义：由正态曲线可得，随机变量X落在区间（a,b]的概率(图中阴影面积)就是由直线x=a,x=b，x轴以及函数f(x)围成的曲边梯形的面积。问：如何求随机变量X落在区间（a,b]的概率？叫叫叫叫一般地，如果对任何实数,()abab，随机变量X满足dxxfbXaPba)(3.3.正态分布的定义正态分布的定义则称随机变量X服从正态分布（normaldistribution）.记作:2,~NX经验表明，一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和，它就服从或近似服从正态分布.生活中很多随机变量都服从或近似服从正态分布。如：（1）某零件的尺寸；（2）高二5班全体同学的身高、体重、肺活量；（3）这次月考高二5班的数学成绩；（4）一定条件下生长的粮食的单位面积产量；（5）电灯的使用寿命。我们从上图看到，正态总体在(μ－2σ,μ＋2σ)以外取值的概率只有4.6％，在以外取值的概率只有0.3％。3,3;XP;22XP.33XP0.68260.95440.99744.4.特殊区间的概率特殊区间的概率3原则例1：某地区数学考试的成绩X服从正态分布，其密度函数曲线如下图：(1)写出X的正态密度函数；(2)求成绩X位于区间68,52的概率是多少？(3)求成绩X位于区间68,60的概率是多少？102030405060708090100y281xO解：(1)根据对称轴可知60，根据峰值可知8，代入正态曲线表达式可得：128602281xexf,由8,60知：正态分布的实际应用(2)6852XP＜XP＜6826.0(3)6860XP＜685221XP＜3413.0例2：设随机变量X～N(2，σ2)(σ>0)，若X在(0,2)内取值的概率为0.2，试求：(1)X在(0,4)内取值的概率；(2)P(X>4)．利用正态分布的对称性求概率解：(1)由于X～N(2，σ2)，对称轴x＝2，画出示意图， P(04)＝[1－P(0