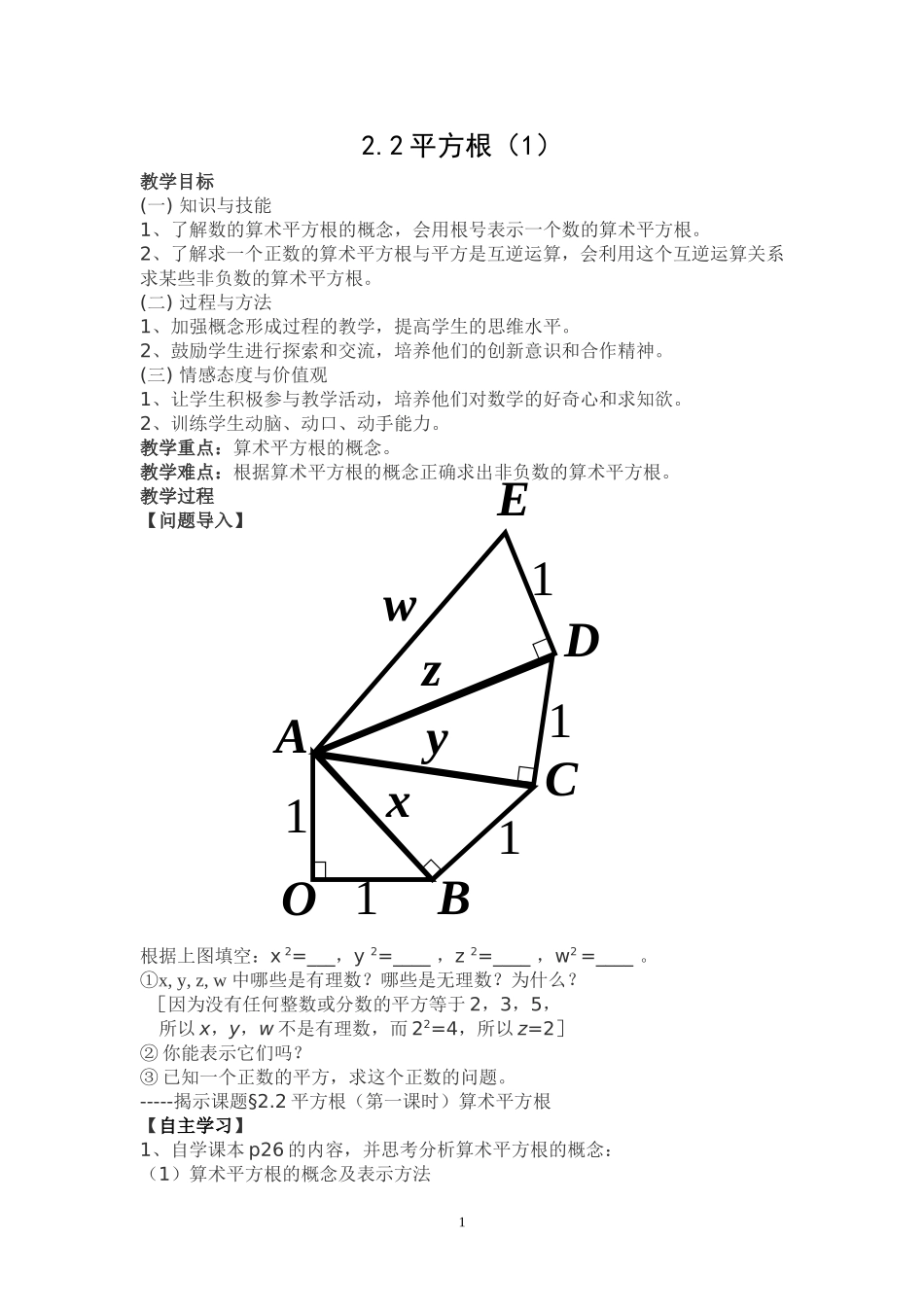
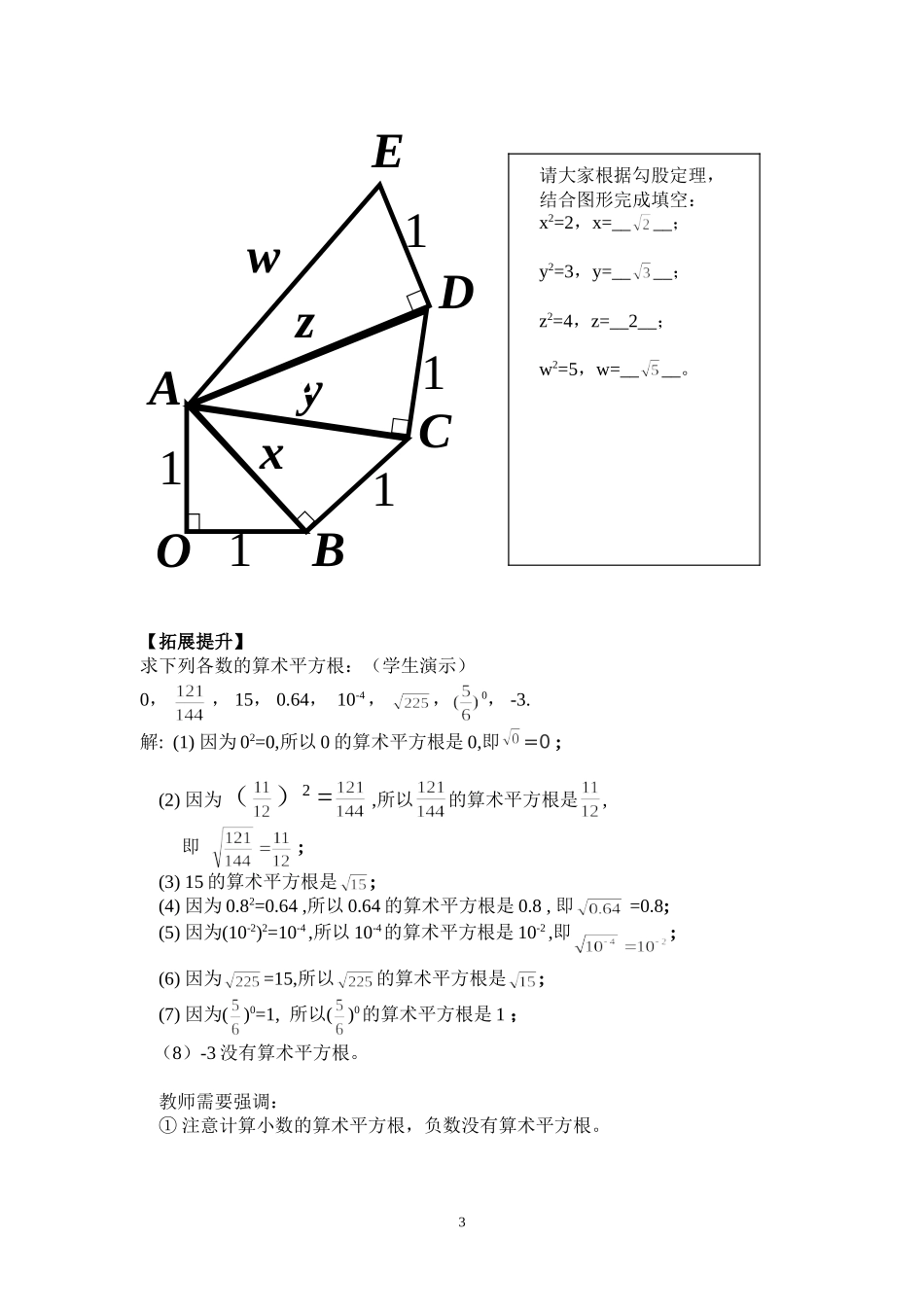
2.2平方根(1)教学目标(一)知识与技能1、了解数的算术平方根的概念,会用根号表示一个数的算术平方根。2、了解求一个正数的算术平方根与平方是互逆运算,会利用这个互逆运算关系求某些非负数的算术平方根。(二)过程与方法1、加强概念形成过程的教学,提高学生的思维水平。2、鼓励学生进行探索和交流,培养他们的创新意识和合作精神。(三)情感态度与价值观1、让学生积极参与教学活动,培养他们对数学的好奇心和求知欲。2、训练学生动脑、动口、动手能力。教学重点:算术平方根的概念。教学难点:根据算术平方根的概念正确求出非负数的算术平方根。教学过程【问题导入】根据上图填空:x2=___,y2=____,z2=____,w2=____。①x,y,z,w中哪些是有理数?哪些是无理数?为什么?[因为没有任何整数或分数的平方等于2,3,5,所以x,y,w不是有理数,而22=4,所以z=2]②你能表示它们吗?③已知一个正数的平方,求这个正数的问题。-----揭示课题§2.2平方根(第一课时)算术平方根【自主学习】1、自学课本p26的内容,并思考分析算术平方根的概念:(1)算术平方根的概念及表示方法111111ABOCDExyzw如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根,记作“”,读作“根号a”。特别地,我们规定:0的算术平方根是0,即=0。(2)式子的两层含义:1)a≥0;2)≥02、例1求下列各数的算术平方根:(1)900(2)1(3)(4)14解:(1)因为302=900,所以900的算术平方根是30,即=30;(2)因为12=1,所以1的算术平方根是1,即=1;(3)因为()2=,所以的算术平方根是,即=;(4)14的算术平方根是。教师需要强调:非平方数的算术平方根只能用根号表示。【交流合作】(小组内交流,互评对错,并帮助改正,分析错误原因,加以总结)①通过例题1,思考一下,我们在求算术平方根时是借助于哪一种运算来求的?[是通过平方来求的.]②求一个正数的平方的运算和求算术平方根的运算的关系怎样?教师点拨:由此我们可以看出一个正数的平方和求算术平方根是互为逆运算而且在例题中的步骤采取语言叙述和符号表示互相补充的做法,目的是让学生明白算术平方根的概念,以及从计算中进一步体会一个正数的平方和求算术平方根是互为逆运算,在以后的步骤中可以简化。3、例2自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2.有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?教师点拨:例2中的19.6米表示什么?(自由下落物体下落的距离s)解:将s=19.6代人s=4.9t2中,得到t2=4,根据算术平方根的定义,t==2(秒)4、解决引例2【拓展提升】求下列各数的算术平方根:(学生演示)0,,15,0.64,10-4,,0,-3.解:(1)因为02=0,所以0的算术平方根是0,即=0;(2)因为()2=,所以的算术平方根是,即;(3)15的算术平方根是;(4)因为0.82=0.64,所以0.64的算术平方根是0.8,即=0.8;(5)因为(10-2)2=10-4,所以10-4的算术平方根是10-2,即;(6)因为=15,所以的算术平方根是;(7)因为()0=1,所以()0的算术平方根是1;(8)-3没有算术平方根。教师需要强调:①注意计算小数的算术平方根,负数没有算术平方根。11111ABOCDExyzzzw3请大家根据勾股定理,结合图形完成填空:x2=2,x=____;y2=3,y=____;z2=4,z=__2__;w2=5,w=____。②注意计算0的算术平方根时,要先算出它们的值,然后再计算算术平方根。【课堂小结】你今天有什么收获与感悟?本节课学习了算术平方根的概念和表示方法,理解了求一个非负数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根。【课后作业】p27习题2.3【板书设计】平方根(1)引例----------------------例1----------------知识拓展----------------------------------------------------------------------------算术平方根的概念例2----------------小结---------------------------------------------------------------------------------------------------------------解决引例-----------作业---------------------------------------------------4