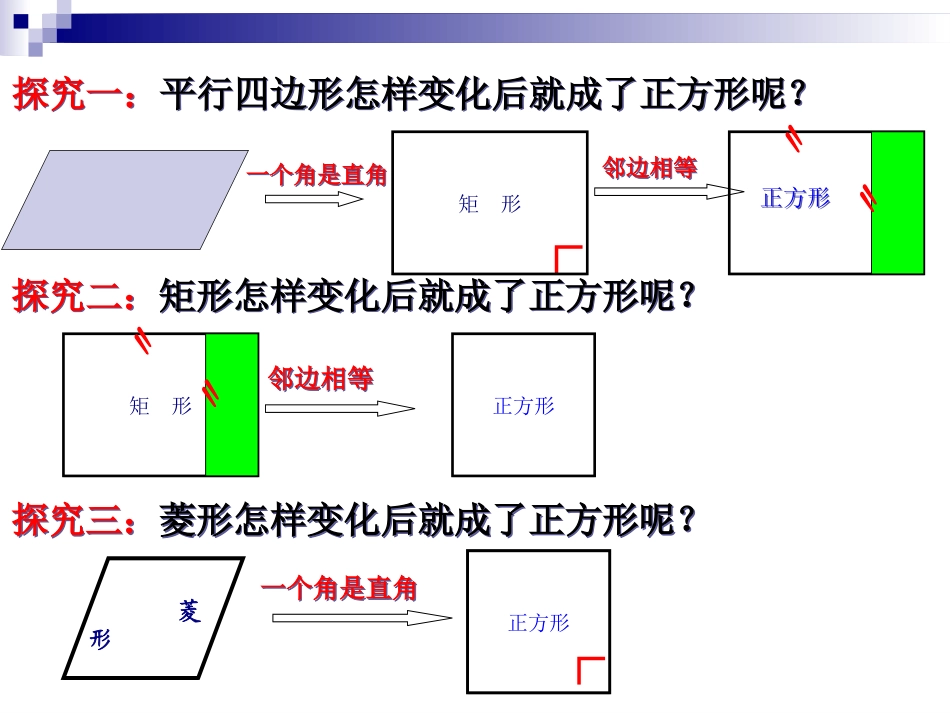
知识回顾:定义边角对角线对称性平行四边形矩形菱形几种特殊四边形的定义及性质对边平行且相等对边平行且相等对边平行,四边都相等对角相等,邻角互补四个角都是直角对角相等,邻角互补对角线互相平分对角线相等且互相平分对角线互相垂直平分,每条对角线平分一组对角中心对称图形轴对称图形、中心对称图形轴对称图形、中心对称图形两组对边边分别平行的四边形两组对边边分别平行的四边形有一个角角是直角的平行四边边形有一个角角是直角的平行四边边形有一组邻邻边相等的平行四边边形有一组邻邻边相等的平行四边边形探究一:平行四边形怎样变化后就成了正方形呢?探究一:平行四边形怎样变化后就成了正方形呢?探究二:矩形怎样变化后就成了正方形呢?探究二:矩形怎样变化后就成了正方形呢?探究三:菱形怎样变化后就成了正方形呢?探究三:菱形怎样变化后就成了正方形呢?矩形正方形邻边相等邻边相等〃〃菱形一个角是直角一个角是直角正方形∟∟矩形正方形正方形〃〃一个角是直角一个角是直角邻边相等邻边相等(可从平行四边形,矩形,菱形入手判别)(可从平行四边形,矩形,菱形入手判别)有一组邻边相等并且有一个角是直角的平行四边形是正方形有一组邻边相等并且有一个角是直角的平行四边形是正方形有一组邻边相等的矩形是正方形有一组邻边相等的矩形是正方形有一个角是直角的菱形是正方形有一个角是直角的菱形是正方形正方形有哪些性质?正方形有哪些性质?正方形的性质=矩形的性质+菱形的性质正方形的性质=矩形的性质+菱形的性质正方形性质边角对角线对称性图形语言文字语言符号语言ACD\BACDBACDB\\\∟∟∟∟O\\\\∟对边平行,四条边都相等四个角都是直角对角线互相垂直平分且相等,每条对角线平分一组对角∵四边形ABCD是正方形∴ABCD∥ADBC,∥AB=BC=CD=AD∵四边形ABCD是正方形∴∠A=B=C=∠∠D∠=90°∵四边形ABCD是正方形∴ACBD,AC=BD,⊥OA=OB=OC=OD,∠1=2=3=4=∠∠∠5=6=7=8∠∠∠∠轴对称图形中心对称图形1122334455667788平行四边形矩形菱形正方形请填写正方形、菱形、矩形、平行四边形的关系图请填写正方形、菱形、矩形、平行四边形的关系图认真观察,你会有发现!认真观察,你会有发现!一个正方形绕对角线的交点旋转多少度可以重合?一个正方形绕对角线的交点旋转多少度可以重合?例例求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.ADCBO已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O.求证:ABO△、△BCO、△CDO、△DAO是全等的等腰直角三角形.分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.ADCBO正方形对角线把正方形分成多少个等腰直角三角形?拓展讨论:结论:分成八个等腰直角三角形,分别是△ABC、△ADC、△ABD、△BCD;△AOB、△BOC、△COD、△DOA.例2(补充)已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DGAE⊥于G,DG交OA于F.例2(补充)已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DGAE⊥于G,DG交OA于F.求证:OE=OF.分析:要证明OE=OF,只需证明△AEODFO≌△,由于正方形的对角线垂直平分且相等,可以得到∠AOE=DOF=90°∠,AO=DO,再由同角或等角的余角相等可以得到∠EAO=FDO∠,根据ASA可以得到这两个三角形全等,故结论可得.求证:OE=OF.分析:要证明OE=OF,只需证明△AEODFO≌△,由于正方形的对角线垂直平分且相等,可以得到∠AOE=DOF=90°∠,AO=DO,再由同角或等角的余角相等可以得到∠EAO=FDO∠,根据ASA可以得到这两个三角形全等,故结论可得.小结1、正方形定义有一组邻边相等并且有一个角是直角的平行四边形是正方形2、正方形有哪些性质?对边平行,四条边都相等四个角都是直角对角线互相垂直平分且相等,每条对角线平分一组对角边:角:对角线: